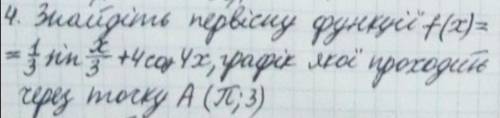
Объяснение:
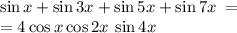
Проведем доказательство тождества следующим образом:
- проведем равносильные преобразования левой части доказываемого тождества;
- если в итоге преобразований левая часть примет ту же форму что и правая часть - тождество доказано.
Итак - левая часть:
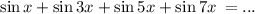
Сгруппируем следующим образом:
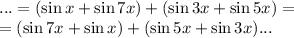
Воспользуемся формулой суммы синусов:
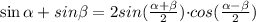
Поочередно сложим группы внутри скобок:
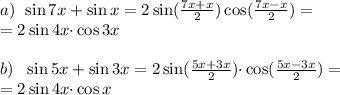
Тогда вся левая часть примет вид:
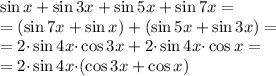
для преобразования суммы косинусов в скобках воспользуемся такой формулой:
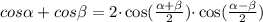
Выражение примет вид:
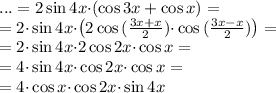
В результате преобразований левая часть приняла тот же вид что и правая.
Тождество доказано.
Дробь
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то