(1) Подкоренное выражение должно быть неотрицательным.
(2) Знаменатель дроби не должен быть равен нулю.
Учитывая их, записываем следующую систему.
Для начала решим отдельно верхнее неравенство системы. Его можно решить методом интервалов, предварительно разложив на множители числитель и знаменатель.
Числитель мы разложили по формуле сокращённого умножения (разность квадратов). Для разложения знаменателя понадобится найти корни следующего уравнения:
Используя следующую формулу: , где и - корни уравнения , получаем: , здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
Решим данное неравенство методом интервалов.
Нули числителя: -3; 3.
Нули знаменателя: 2; 4.
- + - + -
----------------------------------о----------------------------------о-----------------> x
Так как знак в последней строке неравенства "больше или равно", то подходят те промежутки, где стоит знак "плюс". В нашем случае: .
Решением нижнего выражения являются и . В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
Всего 10-значных чисел 9*10^9 Посчитаем, сколько из них чисел, у которых все цифры разные. На 1 месте может стоять любая цифра, кроме 0. 9 вариантов. На 2 месте любая, кроме той, что стоит на 1 месте. 9 вариантов. На 3 месте любая, кроме двух первых. 8 вариантов. И так далее. На 9 месте любая, кроме 8 первых. 2 варианта. На 10 месте стоит одна последняя цифра. 1 вариант. Всего 9*9*8*7*...*2*1 = 9*9! = 3265920 Итак, мы получили: всего 10-значных чисел 9*10^9 = 9000000000 Из них 3265920 чисел, состоящих из всех 10 разных цифр. У остальных 9000000000 - 3265920 = 8996734080 чисел повторяется хотя бы одна цифра.
X^2+y^2=1 Окружность с центром в начале координат и радиусом R=1.
1) Если вам надо решить именно через производную, то самое расстояние будет касательной проведенной из точки (2,0) к данной окружности Рассмотрим его одну полуокружность y=√(1-x^2) (так как симметричны) Если A(a,√(1-a^2)) точки касания, то f(a)=√(1-a^2) f'(a)=-a/√(1-a^2) тогда уравнение касательной y=(1-ax)/√(1-a^2) она проходит через точку (2,0) то есть 0=(1-2a)/√(1-a^2) откуда a=1/2 то есть точки касания A(1/2,√(3)/2) B(2,0) откуда расстояние AB=√(9/4+3/4) = √(3) (наибольшее как касательная)
2) Если геометрический то получаем гипотенузу расстоянием AB=2, AC=1 тогда второй катет BC=√(AB^2-AC^2)=√(4-1)=√(3)
Нужно взять во внимание два условия.
(1) Подкоренное выражение должно быть неотрицательным.
(2) Знаменатель дроби не должен быть равен нулю.
Учитывая их, записываем следующую систему.
Для начала решим отдельно верхнее неравенство системы. Его можно решить методом интервалов, предварительно разложив на множители числитель и знаменатель.
Числитель мы разложили по формуле сокращённого умножения (разность квадратов). Для разложения знаменателя понадобится найти корни следующего уравнения:
Используя следующую формулу: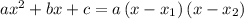 , где
, где 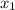 и
и 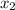 - корни уравнения
- корни уравнения 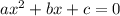 , получаем:
, получаем: 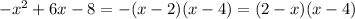 , здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
, здесь минус я занесла в первую скобку. Возвращаемся к неравенству.
Решим данное неравенство методом интервалов.
Нули числителя: -3; 3.
Нули знаменателя: 2; 4.
- + - + -
----------------- -----------------о-----------------
-----------------о----------------- -----------------о-----------------> x
-----------------о-----------------> x
Так как знак в последней строке неравенства "больше или равно", то подходят те промежутки, где стоит знак "плюс". В нашем случае: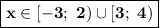 .
.
Решением нижнего выражения являются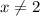 и
и 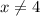 . В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
. В решении неравенства выше эти два значения и так выколоты (стоят круглые скобки), поэтому область определения таковой и остаётся.
ответ: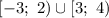 .
.