ответ: 5*a=2*b; 3*a+3=2*b+2⇒b-3*a=1⇒5*a-3*a=2*a=1⇒a=0,5⇒b=5*a/2=5*0,5/2=1,25. Тогда a+b=0,5+1,25=1,75
ответ: 1,75.
Объяснение:

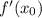 производная функции в данной точке. А
производная функции в данной точке. А  точка касания по иксу.
точка касания по иксу. мы должны найти производную общего типа этой функции.
мы должны найти производную общего типа этой функции.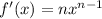 - где n это степень.
- где n это степень.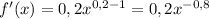


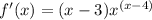
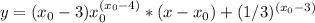
 и получаешь уравнение касательной.
и получаешь уравнение касательной.
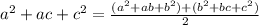

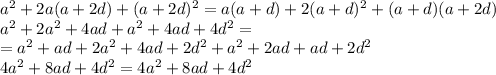
a+b = 7/4
Объяснение:
Так как у нас a/b = 2/5, то 5a = 2b. Отметим это (*)
Следующее. a+1/b+1 = 2/3. ->
3(a+1) = 2(b+1)
3a+3=2b+2
3a+1=2b (*)
3a+1=5a
Отсюда:
5a-3a=1
2a=1
a=1/2
Находим b: из (*)
5*1/2 = 2b
Отсюда 2b = 5/2
b = 5/2 * 1/2 = 5/4
Осталось найти сумму:
a+b = 1/2 + 5/4 =2/4 + 5/4 = 7/4
Проверка:
a/b = 2/5
1/2 / 5/4 = 1/2 * 4/5 = 4/10 или 2/5.