ответ: 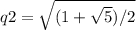
Объяснение:
Пусть самый короткий катет равен b1- первый член геометрической прогрессии, а его квадрат b1².
Тогда второй член геометрической прогрессии - больший катет равен b1·q ( q -знаменатель прогрессии). Тогда его квадрат равен
b1²·q². Тогда 3-ий член геометрической прогрессии - гипотенуза равен b1·q² , а его квадрат равен 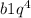
Тогда по теореме Пифагора
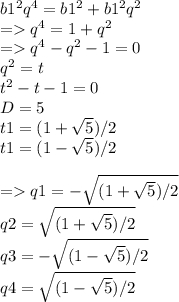
q3 и q4 не годятся , так как число под корнем не может быть меньше 0.
q1 не годится, так как знаменатель не может быть В ДАННОМ СЛУЧАЕ меньше 0 , иначе второй катет будет меньше 0, что быть не может.
Остается только q2
Давайте спростимо дроби та вирази:
а) (a+√7) / (a²-7)
Це рівносильно формі (a + √7) * (1 / (a² - 7)), яка в свою чергу є формою (a + √7) * (1 / (a - √7) * (a + √7)).
Це дозволяє нам спростити вираз до (1 / (a - √7)).
б) (√3 + √15) / (2 + 2√5)
Цей вираз можна спростити, помноживши чисельник і знаменник на спряжене число до знаменника (2 - 2√5):
[(√3 + √15) * (2 - 2√5)] / [(2 + 2√5) * (2 - 2√5)]
Це дає нам:
[(2√3 - 2√15 + 2√15 - 10) / (4 - 20)] =
[(2√3 - 10) / -16] =
-1/8√3 + 5/8
в) (m - 5) / (√m + √5)
Тут також використовуємо метод спряжених чисел, множимо чисельник і знаменник на (√m - √5):
[(m - 5) * (√m - √5)] / [(√m + √5) * (√m - √5)] =
[(m√m - m√5 - 5√m + 25) / (m - 5)] =
√m - √5 + 25/(m - 5)
Спростимо вирази:
√a(√a + 3) - a
Це спрощується до:
a + 3√a - a = 3√a
(√2 - √18)*√2
√18 = √(9*2) = 3√2, отже:
(√2 - 3√2) * √2 = -2√2 * √2 = -4
(3 - √5)² + 6√5
Спрощуємо це:
[(9 - 2*3√5 + 5) + 6√5] =
[14 - 6√5 + 6√5] = 14
(х+1) (х-2)