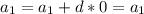Алгебра: Найдите значение выражения: 1/4x³ + 3y² при x= -2 и y= -1

Найдите значение выражения: 1/4x³ + 3y² при x= -2 и y= -1

👇

Увидеть ответ

Ответ:

olga7882

04.04.2020

ответ -8+3*1=
=1/4-8+3=
=1

4,4(95 оценок)

Ответ:

ArtemRussia

04.04.2020

1/4*(-2)3+3*(-1)2=1/4*(-8)+3=-8/4+3=(12-8)/4=4/4=1

4,6(52 оценок)

Открыть все ответы

Ответ:

лулу36

04.04.2020

1)
База индукции: 1

a_1=a_1+d*0=a_1

проверено.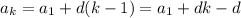

Предположим, что утверждение верно для n=k.
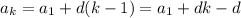$a_{k}=a_1+d(k-1)=a_1+dk-d$
Покажем, и докажем, что утверждение верно так же для n=k+1.
$a_{k+1}=a_1+d[(k+1)-1]=a_1+dk$
Так как , следуя предположению $a_{k}=a_1+d(k-1)=a_1+dk-d$ то прибавив к данному выражению d. Мы получим следующий член $a_{k+1}=a_1+d[(k+1)-1]=a_1+dk$ .
Т.е. предположение верно. Ч.Т.Д.

2)
$S_n= \frac{n[2a_1+d(n-1)]}{2}$
База : 1
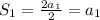Проверка: $S_1= \frac{2a_1}{2}=a_1$ .

Предположение: $n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}$

Теперь покажем и докажем, что данное выражение верно и при n=k+1

:

Так как предыдущий член был равен k, то что бы узнать сумму первых k+1 членов, достаточно прибавить k+1 член (используя формулу которую мы доказали ранее):
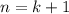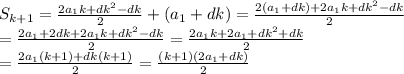
$S_{k+1}= \frac{2a_1k+dk^2-dk}{2}+(a_1+dk)= \frac{2(a_1+dk)+2a_1k+dk^2-dk}{2}\\= \frac{2a_1+2dk+2a_1k+dk^2-dk}{2}= \frac{2a_1k+2a_1+dk^2+dk}{2}\\
= \frac{2a_1(k+1)+dk(k+1)}{2}= \frac{(k+1)(2a_1+dk)}{2}$
т.е. мы пришли к изначальной формуле, если туда подставить k+1. Ч.Т.Д.

3)
Это не формула общего члена, это формула суммы.
При
q=1

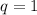получается деление на ноль, поэтому сразу пишем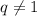 $q \neq 1$
База: 1
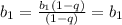
$b_1= \frac{b_1(1-q)}{(1-q)}=b_1$
Предположим, что формула верна для: n=k

Покажем и докажем что формула верна для n=k+1

:
Как и с суммой арифм.прогрессии. Мы добавим k+1 член к сумме.
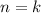
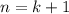$b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}$
Ч.Т.Д.

4,4(66 оценок)

Ответ:

kornsergo23

04.04.2020

Коли дивишся на запорожця на картині Монастирського, то перш за все починаєш пригадувати, чи бачив ти таких людей у житті: він здається небагатослівним і дуже незвичної зовнішності. Найбільше увага затримується на бритій голові і оселедцю. А потім вже помічаєш і пишні вуса, і козацьку шаблю, на яку оперся запорожець.

Невідомо, чи він високого зросту, але мені здається, що він мав би бути приблизно 180 см. Бачу, що він має широкі плечі і міцні руки.

В одязі вояк дуже акуратний. Біла сорочка виразно відтіняє жупан і хутровий кунтуш. Тут дуже майстерно художник використав поєднання чорного і червоного – кольорів прапору Запорізької Січі, кольорів прапору сучасної ОУН-УПА.

Я не знаю його думок, але вираз вольового обличчя показує: про що б він не думав у цю хвилину, зображену на картині, - ці думки про минуле і майбутнє України. Може, саме у ці хвилини він згадує свою дружину, яку залишив у своєму рідному селі? Може, пригадує свою останню зустріч з батьком, який перед походом давав йому настанови про товариські звичаї на Січі? А, може, перед очима стоїть його рідний син, який сьогодні був у першому своєму бою, і тепер запорожець розмірковує, чи достатньо войовничого козака він виростив? А, може, чоловік, як у молитві, зупинився, щоб подякувати Богові за прожитий день?

Брови зведені так, ніби він хоче у кожного глядача спитати: «Чи пам’ятаєш ти про своїх предків? Про те, як ми боролись за нашу волю? Чи вірний ти своїй державі?» Коли дивишся на нього, то хочеться стати струнко і сказати: «Героям слава!»

4,6(11 оценок)

Это интересно:

Компьютеры-и-электроника

21.04.2022

Как победить Анкано в Skyrim...

15.01.2022

Как довольствоваться тем, что у вас есть...

Взаимоотношения

29.10.2021

Как отказаться от мысли об измене партнеру...

Компьютеры-и-электроника

04.10.2022