Первое уравнение - график окружности с центром в точке (0;0), то есть в начале координат, радиусом 3.
Второе уравнение y=x^2+p, график параболы, ветви которой направлены вверх, и которая двигается по оси Oy вверх или вниз(но не влево и вправо) в зависимости от значения p. Парабола будет иметь с графиком окружности 3 точки пересечения (а значит и система будет иметь три решения), когда вершина параболы будет лежать на окружности, а две ветви параболы будут пересекать окружность в 2 точках. Вершина параболы должно лежать в точке (0; -3) чтобы это выполнялось, а значит p=-3
P.S. если что-то не понятно, напишите.

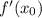 производная функции в данной точке. А
производная функции в данной точке. А  точка касания по иксу.
точка касания по иксу. мы должны найти производную общего типа этой функции.
мы должны найти производную общего типа этой функции.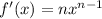 - где n это степень.
- где n это степень.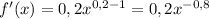


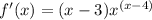
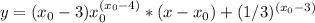
 и получаешь уравнение касательной.
и получаешь уравнение касательной.
В первом примере неопределенность 0 на 0, во втором бесконечность на бесконечность