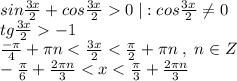
y = -6·x
Объяснение:
Пусть линейные функции, то есть прямые заданы уравнениями y₁=k₁·x+b₁ и y₂=k₂·x+b₂. Прямые параллельны тогда и только тогда, когда k₁=k₂ и b₁≠b₂. Если k₁=k₂ и b₁=b₂, то прямые совпадают.
В силу этого, уравнение прямой, параллельной графику функции y=-6·x+10 имеет вид: y=-6·x+b. Так как прямая проходит через начало координат О(0; 0), то подставляя эти значения определяем b:
0=-6·0+b или b=0.
Тогда уравнение прямой, параллельной графику функции y=-6x+10 и проходящей через начало координат имеет вид: y=-6·x.
10 / 25-х^2 - 1/5 + х / х-5 =0
10 / (5-х)(5+х) - 1/5 + х / х-5 =0
10 / (5-х)(5+х) - 1/5 - х / 5-х =0
Общий знаменатель будет 5(5-х)(5+х)
Домножим числитель первой дроби на 5, второй на (5-х)(5+х), третей на 5(5+х)
Получаем общий числитель Знаменатель
50-5(25-х^2)-5х(5+х) = 0 5(5-х)(5+х)=0
50-125+5х^2-25х-5х^2=0 5-х не равно 0 5+х не равно 0
25х=75 х не равен 5 х не равен -5
х=3