х = 32, у = 29.
Объяснение:
Записываем условие:
x - y = 3
x^2 - y^2 = 183
Выражаем y через х из первого уравнения.
y = x - 3
Заменяем y во втором уравнении.
x^2 - (x - 3)^2 = 183
Раскрываем x - 3 по правилу сокращенного умножения
(a - b)^2 = a^2 - 2ab + b^2
(x - 3)^2 = x^2 - 6x + 9
Записываем все в одно уравнение:
x^2 - (x^2 - 6x + 9) = 183
Раскрываем скобки, меняя знаки.
x^2 - x^2 + 6x - 9 = 183
6x - 9 = 183
6x = 192
x = 192/6 = 32
Следовательно y = x - 3 = 32 - 3 = 29.
Проверяем:
32 - 29 = 3
32^2 = 1024; 29^2 = 841; 1024 - 841 = 183
Все верно.
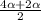 sin
sin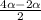 =2cos3α*sinα
=2cos3α*sinα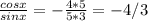
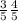 =-24/25
=-24/25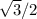
1) f'(x)=-1/(1-x)=1/(x-1)
k=-1 1/(x-1)=-1 x-1=-1 x=0
f(0)=ln1=0
y=-x
2) k=3
3/(3x-2)=3 3=9x-6 9=9x x=1
f(1)=ln1=0
y=3x+c 0=3*1+c c=-3
y=3x-3
3) f'=(2x-2)/(x^2-2x-3)
3y=1-2x y=-2/3x+1/3
(x-1)/(x^2-2x-3)=-1/3
3x-3=-x^2+2x+3
x^2+x-6=0
x=-3 x=2
y(2)=ln(-3) не существует
y(-3)=ln(9-3+6)=ln12
ln12=-2/3(-3)+c
ln12=2+c x=ln12-2
y=-2/3x+ln12-2
4) (-2x-2)/(3-2x-x^2)
2/3x-1/3=y
(x+1)/(x^2+2x-3)=1/3
3x+3=x^2+2x+3
x^2-x=0
x=1 x=0
f(0)=ln3
y=2/3x+c
y=2/3x+ln3.