Задача: Сумма катетов прямоугольного треуольника равна 24 см. Найти длины катетов этого треугольника, при которых площадь треугольника будет наибольшей.
Пусть один катет будет x cm, тогда второй — 24−x cm. составим уравнение для вычисления площади прямоугольного т-ка, где x — независимая переменная, S — зависимая переменная:
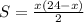
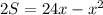
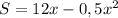
Графиком данной функции является парабола.
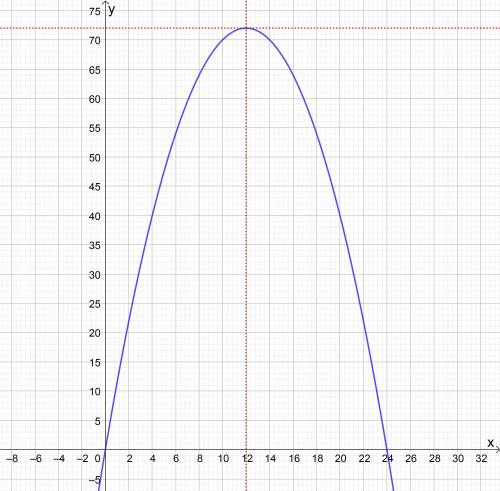
Определим вершину параболы, построим график функции S(x):
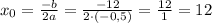
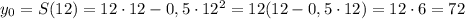
Ордината вершины параболы — и есть максимальная площадь треугольника. Абсцисса вершины — значение, которое принимает независимая переменная, то есть один из катетов прямоугольного треугольника, который мы обозначили за x.
Из графика видно, что длины катетов треугольника будут равны, и равны абсциссе вершины параболы.
Или выведем аналитически:
если один катет x = 12 cm, тогда второй 24−x = 24−12 = 12 cm
ответ: Катеты треугольника должны быть равны 12 и 12 см.
Максимальная площадь равна 72 см².
(4;-5)
Або по іншому:
х = 4
у = -5
Объяснение:
Розписую пошагово. Якщо не зрозуміло , питайте..
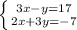 (в верхньому рівнянні знаходимо "у")
(в верхньому рівнянні знаходимо "у")
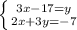 ( верхньому рівнянні перекинули "у" вправо, а 17 вліво змінивши на них знаки)
( верхньому рівнянні перекинули "у" вправо, а 17 вліво змінивши на них знаки)
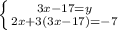 (підставляємо наш "у", який дорівнює (3х-17) в нижнє рівняння)
(підставляємо наш "у", який дорівнює (3х-17) в нижнє рівняння)
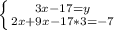 (розкриваємо дужки в нижньому рівнянні)
(розкриваємо дужки в нижньому рівнянні)
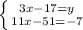 (вирішуємо нижнє рівняння)
(вирішуємо нижнє рівняння)
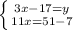
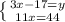
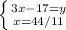
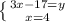
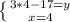 (підставляємо знайдений "х" в верхнє рівняння)
(підставляємо знайдений "х" в верхнє рівняння)
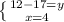
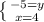
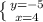
Перевіряємо підставляючи замість невідомих "х" та "у" знайдені числа::
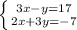
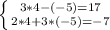
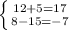
- 6 - 6X < - 5X + 6
-6X + 5X < 6 + 6
- X < 12
X < ( - 12 )
ответ: ( - бесконечность ; - 12 )