х = 32, у = 29.
Объяснение:
Записываем условие:
x - y = 3
x^2 - y^2 = 183
Выражаем y через х из первого уравнения.
y = x - 3
Заменяем y во втором уравнении.
x^2 - (x - 3)^2 = 183
Раскрываем x - 3 по правилу сокращенного умножения
(a - b)^2 = a^2 - 2ab + b^2
(x - 3)^2 = x^2 - 6x + 9
Записываем все в одно уравнение:
x^2 - (x^2 - 6x + 9) = 183
Раскрываем скобки, меняя знаки.
x^2 - x^2 + 6x - 9 = 183
6x - 9 = 183
6x = 192
x = 192/6 = 32
Следовательно y = x - 3 = 32 - 3 = 29.
Проверяем:
32 - 29 = 3
32^2 = 1024; 29^2 = 841; 1024 - 841 = 183
Все верно.
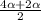 sin
sin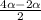 =2cos3α*sinα
=2cos3α*sinα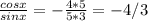
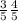 =-24/25
=-24/25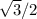
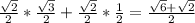
x=42, y=39
Объяснение:
Будем работать со вторым уравнением.
Оставим пока так. Работаем с первым уравнением. Получаем:
Получается, что правые части обоих уравнений равноценны ( так как равны x+y )
Умножим на x-y
Исходя из этого:
x-y=3
Получается
Подставим это в 1 уравнение ( самое первое ), тогда
Значит x+y=81
Делаем систему уравнений из двух получившихся уравнений
Находим y, путем переноса -y в правую часть уравнения
Подобные складываем, 3 переносим вправо.