В решении.
Объяснение:
Решите задачу с составления уравнения. Разность двух чисел равна 25, а разность их квадратов 875. Найдите эти числа.
х - первое число.
у - второе число.
По условию задачи система уравнений:
х - у = 25
х² - у² = 875
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 25 + у
(25 + у)² - у² = 875
625 + 50у + у² - у² = 875
50у = 875 - 625
50у = 250
у = 250/50
у = 5 - второе число.
х = 25 + у
х = 25 + 5
х = 30 - первое число.
Проверка:
30 - 5 = 25, верно.
30² - 5² = 900 - 25 = 875, верно.
Эту задачу можно решить из условия, что прямая 4х+3у=к является касательной к гиперболе ху = 3. При этом 1 решение в точке касания.
Уравнение гиперболы можно представить так: у = 3/х.
Производная этой функции равна y' = -3/x².
Прямая с угловым коэффициентом имеет вид у = (-4/3)х + (к/3).
Производная равна угловому коэффициенту касательной.
-3/x² = -4/3.
4x² = 9.
х = +-(2/3).
у = 3/(+-(2/3) = +-2. Это координаты точек касания.
Подставим эти значения в уравнение заданной прямой.
+-2 = (-4/3)*(+-(3/2) + (к/3).
+-2 = -+2 + (к/3).
(к/3) = +-4.
к = +-12.
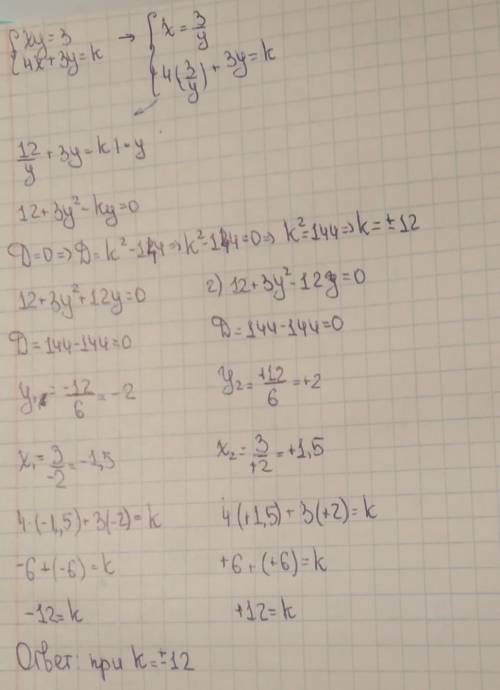
По-моему знак неравенства
Любое число в квадрате равно положительному значению или нулю, поэтому всё выражение либо больше, либо равно нулю