Дана функция y(x)= –2·x–3.
1) y(1)= –2·1–3= –2–3= –5; y(–1)= –2·(–1)–3= 2–3= –1;
y(0)= –2·0–3= 0–3= –3; y(–1/2)= –2·(–1/2)–3= 1–3= –2;
2) Определим значения x, при которых y(x)=1:
–2·x–3=1 ⇔ –2·x= 1+3 ⇔ –2·x= 4 ⇔ x= –2;
Определим значения x, при которых y(x)= –1:
–2·x–3= –1 ⇔ –2·x= –1+3 ⇔ –2·x= 2 ⇔ x= –1;
Определим значения x, при которых y(x)=0:
–2·x–3=0 ⇔ –2·x= 3 ⇔ x= –3/2;
3) Определим значения x, при которых функция принимает отрицательные значения, то есть решаем неравенство y(x)<0:
–2·x–3<0 ⇔ –3 < 2·x ⇔ –3/2 < x ⇔ x∈(–3/2; +∞).
Объяснение:
5.
пусть скорость катера в посёлок равна Х км/ч , тогда из посёлка она равна (Х-34) км/ч
Расстояние за формулой равно:
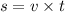
где s - расстояние; v-скорость ; t-время , за которое он проплыл это расстояние при определённой скорости
расстояние когда катер плыл в посёлок:
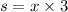
расстояние когда катер плыл обратно:
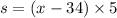
расстояние в посёлок и обратно не изменилось, тогда мы можем приподнять правые части уравнений :
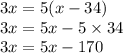
переносим (х) в одну сторону:
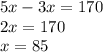
Мы нашли скорость катера когда он плыл в посёлок. теперь найдем расстояние:
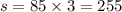
S=255 км
6.
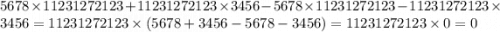
число 11231272123 есть в каждом из слагаемых, по этому вынесем его . у нас останется (5678+3456-5678-3456) , что равно 0. Любое чисто умноженное на 0 равно 0.
7.
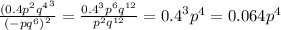
вроде правильно