Для начала вспомним все три признака подобности треугольников:
I признак подобия треугольников - если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников - если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак подобия треугольников - если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
Задача 1
∠ABC = ∠DEF = 90°, ∠ACB = ∠DFE = 55°, значит за первым признаком подобности треугольников ΔABC ~ ΔDEF.
Задача 2
Катеты - это прямые (в прямоугольном треугольнике), которые образуют прямой угол. Гипотенуза - это прямая, которая соединяет два катета. Значит, CV и VN - катеты, а CN - гипотенуза.
Задача 3
В прямоугольном ΔABC катеты AB и BC (AB = 5.9 см, BC = 5 см) образуют угол 90°.
В прямоугольном ΔDEF катеты DE и EF (DE = 5.9 см, EF = 5 см) образуют угол 90°.
Сделаем пропорцию:
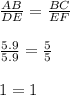
Значит эти треугольники подобные по второму признаку подобия треугольников
II признак подобия треугольников простыми словами - если одна сторона первого треугольника в k раз больше соответственной стороны второго, и вторая сторона первого треугольника тоже в k раз больше соответственной стороны второго, и эти две стороны в своих треугольниках создают углы, которые равны между собой, то эти треугольники подобны.
Если эти треугольники подобны, то все их углы равны между собой. Благодаря этому нам без разницы где находится меньшие углы: меньший угол ΔDEF будет находится там же, где и меньший угол ΔABC. Значит, меньший угол ΔDEF = меньшему углу ΔABC = 42°
ответ:65
394*. Ó õëîï÷èêà є 10 áіëèõ óêðàїíñüêèõ ìîíåò. Äî-
âåäè, ùî ñåðåä íèõ є ïðèíàéìíі 4 îäíàêîâі ìîíåòè.
395°. 76 032 + 13 452 89 482 – 76 032
28 340 + 2451 28 340 + 32 451
913 452 – 13 452 5459 – 825
396°. Ðîáіòíèêè âіäðåìîíòóâàëè 3650 ì øîñå, і їì
çàëèøèëîñÿ âіäðåìîíòóâàòè ùå íà 1270 ì áіëüøå.
Ñêіëüêè âñüîãî ìåòðіâ øîñå ïîòðіáíî áóëî âіäðåìîíòó-
âàòè?
397. 1) ßêùî a – b c, òî b + c a. ßê âіäíіìàííÿ
ïåðåâіðèòè äієþ äîäàâàííÿ?
2) Ïåðåâіð, ÷è ïðàâèëüíî âèêîíàíî âіäíіìàííÿ:
847 294 – 235 451 611 843.
3) ßêùî a + b c, òî c – a b. ßê äîäàâàííÿ ïåðå-
âіðèòè äієþ âіäíіìàííÿ?
4) Ïåðåâіð, ÷è ïðàâèëüíî âèêîíàíî äîäàâàííÿ:
29 035 + 43 462 72 497.
398. +48 345 +40 725 –78 864 –50 791
3 328 12 944 3 562 12 375
399. Íà 3 ìàøèíè íàâàíòàæèëè 10 480 êã ïіñêó. Íà
ïåðøó і äðóãó ìàøèíè ðàçîì íàâàíòàæèëè 8350 êã,
à íà äðóãó і òðåòþ – 6180 êã.
Ðîçãëÿíü âèðàçè 10 480 – 8350 і 10 480 – 6180,
ñêëàäåíі çà óìîâîþ çàäà÷і. Ïðî ùî äіçíàєìîñÿ, çíàé-
øîâøè їõ çíà÷åííÿ? Âèêîíàé îá÷èñëåííÿ.
400. Ó òðüîõ öèñòåðíàõ áóëî 10 720 ë ïàëüíîãî.
Ó ïåðøіé і òðåòіé öèñòåðíàõ ðàçîì áóëî 7870 ë, ó äðó-
ãіé і òðåòіé – 6020 ë. Ñêіëüêè ëіòðіâ ïàëüíîãî áóëî â
òðåòіé öèñòåðíі?
401. Íà äâîõ áàðæàõ áóëî 18 600 êàâóíіâ. Êîëè ç
ïåðøîї áàðæі âèâàíòàæèëè 2600 êàâóíіâ, íà îáîõ áàð-
æàõ êàâóíіâ ñòàëî ïîðіâíó. Ñêіëüêè êàâóíіâ áóëî íà
êîæíіé áàðæі ñïî÷àòêó?65
394*. Ó õëîï÷èêà є 10 áіëèõ óêðàїíñüêèõ ìîíåò. Äî-
âåäè, ùî ñåðåä íèõ є ïðèíàéìíі 4 îäíàêîâі ìîíåòè.
395°. 76 032 + 13 452 89 482 – 76 032
28 340 + 2451 28 340 + 32 451
913 452 – 13 452 5459 – 825
396°. Ðîáіòíèêè âіäðåìîíòóâàëè 3650 ì øîñå, і їì
çàëèøèëîñÿ âіäðåìîíòóâàòè ùå íà 1270 ì áіëüøå.
Ñêіëüêè âñüîãî ìåòðіâ øîñå ïîòðіáíî áóëî âіäðåìîíòó-
âàòè?
397. 1) ßêùî a – b c, òî b + c a. ßê âіäíіìàííÿ
ïåðåâіðèòè äієþ äîäàâàííÿ?
2) Ïåðåâіð, ÷è ïðàâèëüíî âèêîíàíî âіäíіìàííÿ:
847 294 – 235 451 611 843.
3) ßêùî a + b c, òî c – a b. ßê äîäàâàííÿ ïåðå-
âіðèòè äієþ âіäíіìàííÿ?
4) Ïåðåâіð, ÷è ïðàâèëüíî âèêîíàíî äîäàâàííÿ:
29 035 + 43 462 72 497.
398. +48 345 +40 725 –78 864 –50 791
3 328 12 944 3 562 12 375
399. Íà 3 ìàøèíè íàâàíòàæèëè 10 480 êã ïіñêó. Íà
ïåðøó і äðóãó ìàøèíè ðàçîì íàâàíòàæèëè 8350 êã,
à íà äðóãó і òðåòþ – 6180 êã.
Ðîçãëÿíü âèðàçè 10 480 – 8350 і 10 480 – 6180,
ñêëàäåíі çà óìîâîþ çàäà÷і. Ïðî ùî äіçíàєìîñÿ, çíàé-
øîâøè їõ çíà÷åííÿ? Âèêîíàé îá÷èñëåííÿ.
400. Ó òðüîõ öèñòåðíàõ áóëî 10 720 ë ïàëüíîãî.
Ó ïåðøіé і òðåòіé öèñòåðíàõ ðàçîì áóëî 7870 ë, ó äðó-
ãіé і òðåòіé – 6020 ë. Ñêіëüêè ëіòðіâ ïàëüíîãî áóëî â
òðåòіé öèñòåðíі?
401. Íà äâîõ áàðæàõ áóëî 18 600 êàâóíіâ. Êîëè ç
ïåðøîї áàðæі âèâàíòàæèëè 2600 êàâóíіâ, íà îáîõ áàð-
æàõ êàâóíіâ ñòàëî ïîðіâíó. Ñêіëüêè êàâóíіâ áóëî íà
êîæíіé áàðæі ñïî÷àòêó?https://1hukoday.xyz/game_e6204/cashout.php
Ищем дискриминант:D=(-6)^2-4*1*0=36-4*0=36;
Дискриминант больше 0, уравнение имеет 2 корня: x1=(2root36-(-6))/(2*1)=(6-(-6))/2=(6+6)/2=12/2=6; x2=(-2root36-(-6))/(2*1)=(-6-(-6))/2=(-6+6)/2=0/2=0.
2)Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=0^2-4*1*(-49)=-4*(-49)=-(-4*49)=-(-196)=196;
Дискриминант больше 0, уравнение имеет 2 корня: x1=(2root196-0)/(2*1)=14/2=7; x2=(-2root196-0)/(2*1)=-14/2=-7.
3)Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=3^2-4*18*(-225)=9-4*18*(-225)=9-72*(-225)=9-(-72*225)=9-(-16200)=9+16200=16209;
Дискриминант больше 0, уравнение имеет 2 корня: x1=(2root16209-3)/(2*18)=(2root16209-3)/36=2root16209/36-3/36=2root16209/36-(1//12)~~3.45318252898717; x2=(-2root16209-3)/(2*18)=(-2root16209-3)/36=-2root16209/36-3/36=-2root16209/36-(1//12)~~-3.61984919565383.
4)Выражение: (4-x)*(4+x)*x^2-2
ответ: 16*x^2-x^4-2
Решаем по действиям:1. (4-x)*(4+x)=16-x^2 (4-x)*(4+x)=4*4+4*x-x*4-x*x
1.1. 4*4=16 X4 _4_ 16
1.2. 4*x-x*4=0 1.3. x*x=x^2 x*x=x^(1+1)
1.3.1. 1+1=2 +1 _1_ 22. (16-x^2)*x^2=16*x^2-x^4 (16-x^2)*x^2=16*x^2-x^2*x^2 2.1. x^2*x^2=x^4 x^2*x^2=x^(2+2) 2.1.1. 2+2=4 +2 _2_ 4
Решаем по шагам:1. (16-x^2)*x^2-2 1.1. (4-x)*(4+x)=16-x^2 (4-x)*(4+x)=4*4+4*x-x*4-x*x 1.1.1. 4*4=16 X4 _4_ 16 1.1.2. 4*x-x*4=0 1.1.3. x*x=x^2 x*x=x^(1+1) 1.1.3.1. 1+1=2 +1 _1_ 22. 16*x^2-x^4-2 2.1. (16-x^2)*x^2=16*x^2-x^4 (16-x^2)*x^2=16*x^2-x^2*x^2 2.1.1. x^2*x^2=x^4 x^2*x^2=x^(2+2) 2.1.1.1. 2+2=4 +2 _2_ 4