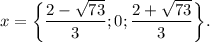Точка x0 называется точкой максимума функции f(x), если существует такая окрестность точки x0, что для всех x ≠ x0 из этой окрестности выполняется неравенство f(x)< f(x0).Точка x0 называется точкой минимума функции f(x), если существует такая окрестность точки x0, что для всех x ≠ x0 из этой окрестности выполняется неравенство f(x)> f(x0).Точки минимума и точки максимума называются точками экстремума.Теорема. Если x0 – точка экстремума дифференцируемой функции f(x), то f ′(x0) =0.Точки, в которых функция имеет производную, равную нулю, или недифференцируема (не имеет производной), называют критическими точками. Точки, в которых производная равна 0, называют стационарными.Геометрический смысл: касательная к графику функции y=f(x) в экстремальной точке параллельна оси абсцисс (OX), и поэтому ее угловой коэффициент равен 0 ( k = tg α = 0).Теорема: Пусть функция f(x) дифференцируема на интервале (a;b), x0 С (a;b), и f ′(x0) =0. Тогда:1) Если при переходе через стационарную точку x0 функции f(x) ее производная меняет знак с «плюса» на «минус», то x0 – точка максимума.2) Если при переходе через стационарную точку x0 функции f(x) ее производная меняет знак с «минуса» на «плюс» , то x0 – точка минимума. ПРАВИЛО нахождения наибольшего и наименьшего значения функции f(x) на отрезке [a;b]. 1. Найти призводную функции и приравнять нулю. Найти критические точки.2. Найти значения функции на концах отрезка, т.е. числа f(a) и f(b).3. Найти значения функции в тех критических точках, которые принадлежат [a;b].4. Из найденных значений выбрать наибольшее и наименьшее. ПРАВИЛО нахождения минимума и максимума функции f(x) на интервале (a;b).1. Найти критические точки f(x) (в которых f ′(x)=0 или f(x) не существует) .2. Нанести их на числовую прямую (только те, которые принадлежат (a,b) ).f ′(x) + – + a x0x1 bf (x) / \ /3. Расставить знаки производной в строке f ′(x) , расставить стрелки в строке f(x).4. x max = x0, x min = x1.5. y max = y(x0), y min = y(x1).
Раскроем скобки:
Приведём подобные слагаемые:
ответ: