Общее расстояние от пункта А до пункта В равно 60*2= 120 км. Время, в которое он ехал со скоростью 60 км/ч неизвестно, значит обозначим его X.
Так как водитель сделал вынужденную остановку на 10 минут, то время всего пути составит 2 часа минус 10 минут, т. е. 11/6 часа. Чтобы узнать время, в которое он ехал со скоростью 80 км/ч, необходимо вычесть из 11/6 число Х. Зная скорости движения и время пути до и после остановки, можем составить уравнение.
60х+80(11/6-х) =120
Решая это уравнение, получим 4/3. Это время, которое он потратил до остановки. Умножаем 60 на 4/3, получаем расстояние 80 км. Это и будет ответом на данную задачу
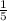 =0,2
=0,2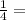 0,25
0,25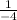
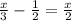
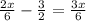
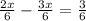
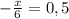
а1=-100
d=8
S=(2a1+d(n-1))*n:2
(2*(-100)+8(n-1))*n:2>0
(-200+8n-8)*n:2>0
(8n-208)*n:2>0
(4n-104)*n>0
4(n-26)*n>0
Рисуем числовую прямую, расставляем на ней две точки выколотые 0 и 26.
Очевидно, что неравенство будет больше нуля, когда n<0 и когда n>26.
Число n должно быть натуральным, поэтому выбираем n>26.
Наименьший n>26 это n=27.
ответ: 27