Дана система уравнений:
{9x^2-42xy+52y^2-6y=265
{3x-7y-11=0.
Заданная система решается методом подстановки.
Из второго уравнения находим у = (3/7)х - (11/7) и подставляем вместо переменной у в первое уравнение.
Вычисление довольно громоздкое.
Результат: х1 = (-31/3), у1 = -6.
х2 = (67/3), у2 = 8.
Первое уравнение - это эллипс, его уравнение линии 2-го порядка задано общим видом Ax² + 2Bx + Cy² + 2Dx + 2Ey + F = 0.
Продольная ось повёрнута от оси Ох на угол, определяемый по формуле tg(2α) = 2B/(A - C) = -42/(9 - 52) = 0,976744186 .
Угол поворота равен 22,163 градуса.
Угол наклона прямой, пересекающей эллипс равен arc tg(3/7) = 23,19859051 градуса.
Во вложении дан график эллипса и прямой.
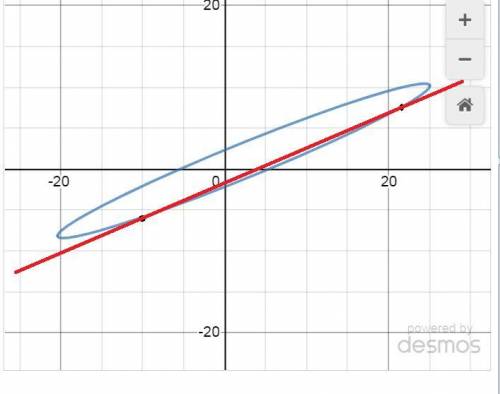
ответ:
tg ∠ spo=sp: op=13: 2=6,5
объяснение:
нарисуем пирамиду, проведем в ней сечение мsk.
мк - средняя линия треугольника cdb, параллельна db и равна ее половине.
диагональ ас квадрата авсd равна диагонали db
ор - четверть этой диагонали и равна 8: 4=2 (из треугольника cdb, в котором высота делится отрезком мк пополам).
sр- высота, биссектриса и медиана треугольного сечения мsk.
небоходимо найти tg ∠ spo, под которым сечение пересекается с плоскостью пирамиды.
нарисуем отдельно треугольник pso.
tg ∠ spo=sp: op=13: 2=6,5
на второй полке х книг , тогда на первой 4х книг
4х-12 = х+12
4х-х =12+12
3х =24
х=24/3
х=8 книг было на второй полке
8*4 = 32 книги было на первой полке