Объяснение:
Решение квадратного неравенства
Неравенство вида
где x - переменная, a, b, c - числа, , называется квадратным.
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения . Для этого необходимо найти дискриминант данного квадратного уравнения. Можно получить 3 случая: 1) D=0, квадратное уравнение имеет один корень; 2) D>0 квадратное уравнение имеет два корня; 3) D<0 квадратное уравнение не имеет корней.
В зависимости от полученных корней и знака коэффициента a возможно одно из шести расположений графика функции
Если требуется найти числовой промежуток, на котором квадратный трехчлен больше нуля, то это числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если требуется найти числовой промежуток, на котором квадратный трехчлен меньше нуля, то это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое - не входят.
Такой метод решения квадратного неравенства называется графическим.
а)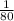
б) 324
Объяснение:
а)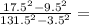
И числитель и знаменатель это формула сокращенного умножения, а точнее разница квадратов. Раскладывается следующим образом:
a² - b² = (a - b) × (a + b)
Сначала разберемся с числителем:
1) 17.5² - 9.5² = (17.5 - 9.5) × (17.5 - 9.5)
2) (17.5 - 9.5) × (17.5 - 9.5) = (8) × (27); (в конце скобки писать не обязательно, это я для наглядности)
Так и оставим пока что. Далее действия со знаменателем:
1) 131.5² - 3.5² = (131.5 - 3.5) × (131.5 + 3.5)
2) (131.5 - 3.5) × (131.5 + 3.5) = (128) × (135); (в конце скобки писать не обязательно, это я для наглядности)
Подставляем числитель и знаменатель:
8 и 128 сокращаются. Так же 27 и 135 сокращаются:
б)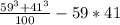
В числителе находится формула сокращенного умножения, а точнее сумма кубов. Раскладывается следующим образом:
а³ + b³ = (a + b) × (a² - ab + b³)
Разберемся с числителем:
1) 59³ + 43³ = (59 + 41) × (59² - 59 × 41 + 41²)
2) (59 + 41) × (59² - 59 × 41 + 41²) = (100) × (59² - 59 × 41 + 41²)
Так пока и оставим (100 не обязательно брать в скобки, это я для наглядности).
Поставим получившийся пример обратно в числитель:
100 и 100 сокращаются:
59² - 59 × 41 + 41² - 59 × 41 = 59² + 41² - 59 × 41 - 59 × 41 (от перемены мест слагаемых сумма не изменяется)
59² + 41² - 59 × 41 - 59 × 41 = 59² - 2 (59 × 41) + 41²
Это разложенный вид формули сокращенного умножения, а точнее квадрата разницы. Складывается следующим образом:
a² - 2ab + b² = (a - b)²
59² - 2 (59 × 41) + 41² = (59 - 41)² = 18² = 324