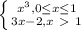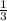ответ: 15 школьников.
Объяснение:
Дано. Число школьников, занимающихся в секции по волейболу относится к числу школьников, занимающихся в секции по футболу, как 3:4.
Сколько школьников занимаются в секции по волейболу, если всего в двух секциях занимаются 35 школьников?
Решение.
Пусть число школьников, занимающихся в секции по волейболу
равно 3х человек. Тогда
в секции по футболу занимаются 4х человек.
3x+4x = 35;
7x=35;
x=5.
Число школьников, занимающихся в секции по волейболу
равно 3*5 = 15 человек.
в секции по футболу занимаются 4х=4*5 = 20 человек.
Найдите f(
)
Обозначим через аi число очков, выбитых первым стрелком при i-м выстреле, а через bi число очков, выбитых вторым стрелком при i-м выстреле.
Тогда из условий задачи следует:
а1+а2+а3= b1+b2+b3, (1)
а3+а4+а5= 3(b3+b4+b5), (2)
Из приведенных попаданий заключаем, что равенство (2) может выполняться, если b1, b2, b3, минимальные по числу очков попадания, а а3, а4, а5 максимальные и сумма а3+а4+а5 кратна трем. Отсюда видно, что b3, b4, b5, это числа 2, 3 и 4, а а3, а4, а5 это числа 10, 9, 8. Далее видим, что первыми четырьмя выстрелами (каждый стрелок сделал по два) они выбили очки: 9, 8, 5, 4. Используем условие (1). Очевидно, что при этом сумма а1+а2 должна быть наименьшей при ее выборе из четырех чисел (9, 8, 5, 4), а b1+b2 наибольший при выборе ее из тех же чисел. Это возможно при a=5, a2=4, a3=10, b1=9, b2=8, b3=2.