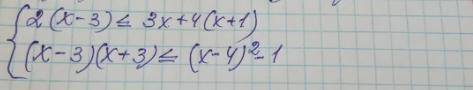
2sin²x+2sinxcos2x-1)/(√cosx)=(2sin²x+2sinxcos2x-1)/(√cosx)=
(2sinxcos2x-cos2x)/(√cosx)=cos2x(2sinx-1)/(√cosx)
ОДЗ : cosx>0;х∈(-π/2+2πm; π/2+2πm); m∈Z;
cos2x=0; х=π/4+πn/2; n∈Z;
sinx=1/2; х=(-1)ⁿπ/6+πк; n∈Z; его лучше расписать для четного и нечетного к. Если к четное , то к=2t; х=π/6+2πt ; t∈Z;
Если к нечетное , то к=2t + 1; х=5π/6+2πt ; t∈Z; этот ответ не подходит, т.к. не входит в ОДЗ.
Найдем корни уравнения из указанного отрезка.
а) х=π/4+πn/2; n∈Z;
2.5π≤π/4+πn/2≤4π; 2.5≤1/4+n/2≤4; 2.25≤n/2≤3.75; 4.5≤n/2≤7.5;
n=5; х=π/4+5π/2=∉ОДЗ,
n=6; х=π/4+6π/2=13π/4∉ОДЗ,
n=7; х=π/4+7π/2=15π/4
б) х=π/6+2πt ;
5/2≤1/6+2t≤4
5/2-1/6≤2t≤4-1/6
7/3≤2t≤23/6
7/6≤t≤23/12 нет здесь корней из указанного отрезка.
Дано:
|y=3x-1
|x+2y=5
Решение
Подставим первое уравнение во второе:
Подставляем полученное значение в первое уравнение:
y=3x-1, при x=1
y=3-1
y=2
ответ: (1;2)
2.
Дано
|x+5y=13
|3x-y=-9
Решение
Выразим из первого уравнения переменную x:
x=13-5y
Подставим полученное выражение во второе уравнение:
3*(13-5y)-y=-9
Раскроем скобки:
39-15y-y=-9
Перенесем неизвестное значение в левую часть, а константы в правую:
-16y=-9-39
y=(-48)/(-16)
y=3
Подставим полученное значение в первое преобразованное уравнение:
x=13-5y, при y=3
x=13-5*3
x=13-15
x=-2
ответ: (-2;3)