1. Точка пересечения графика функции с осью координат Оу:
График пересекает ось Оу, когда x равняется 0: подставляем x=0 в 3x²-x³.
у = 3*0²-0³ = 0,
Результат: y=0. Точка: (0; 0).
2. Точки пересечения графика функции с осью координат Ох:
График функции пересекает ось Ох при y=0, значит, нам надо решить уравнение:
3x²-x³= 0
Решаем это уравнение: 3x²-x³ = х²(3 - x) = 0.
Получаем 2 корня: х = 0 и х = 3.
Результат: y=0. Точки: (0; 0 и (3; 0).
3. Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y' = 6х - 3x² = 0
Решаем это уравнение и его корни будут экстремумами:
3x(2 - х) = 0, получаем 2 точки:
х1 = 0, х2 = 2.
Результат: y’=0. Точки: (0; 0) и (2; 4).
4. Интервалы возрастания и убывания функции:
Найдены 3 интервала монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На этих промежутках находим знаки производной.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = -9 0 3 0 -9
Минимум функции в точке: х = 0,
Максимум функции в точке: х = 2.
Возрастает на промежутке: (0; 2).
Убывает на промежутках: (-∞; 0) U (2; +∞).
5. Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y' '= 6 – 6х = 0.
Решаем это уравнение и его корни будут точками, где у графика перегибы:
6 – 6х = 6(1 – х) = 0.
х = 1. Точка: (1; 2)
6. Интервалы выпуклости, вогнутости:
Найдем интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках изгибов: где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
x = 0 1 2
y'' = 6 0 -6
Вогнутая на промежутках: (-∞; 1).
Выпуклая на промежутках: (1; +∞).
7. Вертикальные асимптоты – нет.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+∞ и x->-∞. Соотвествующие пределы находим:
lim 3x2-x3, x->+∞ = -∞, значит, горизонтальной асимптоты справа не существует
lim 3x2-x3, x->-∞ = ∞, значит, горизонтальной асимптоты слева не существует
Наклонные асимптоты графика функции:
Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при
Находим коэффициент k:
k=lim┬(x→∞)〖(-x^3+3x^2)/x=-∞.〗
Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.
8. Четность и нечетность функции:
Проверим функцию - чётна или нечётна - с соотношений f(-х) = f(x) и f(-х) = -f(x).
Итак, проверяем:
y(-x) = -(-x)³ + 3(-x)² = x³ + 3x² ≠ y(x)
y(-x) = -(-x)³ + 3(-x)² = x³ + 3x² = -(-х³-3х²) ≠ -y(x)
Значит, функция не является ни чётной, ни нечётной.
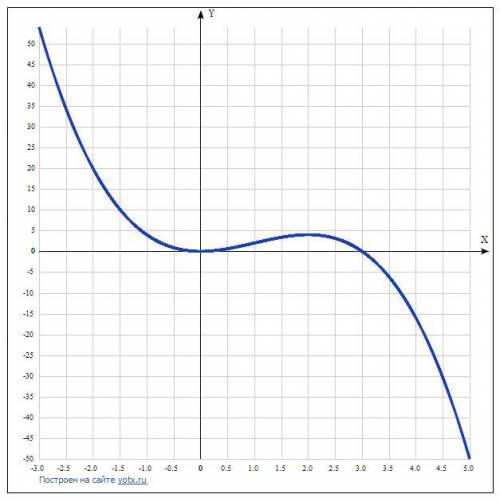
Таблица точек.
x y
-3.0 54
-2.5 34.4
-2.0 20
-1.5 10.1
-1.0 4
-0.5 0.9
0 0
0.5 0.6
1.0 2
1.5 3.4
2.0 4
2.5 3.1
3.0 0
3.5 -6.1
4.0 -16
4.5 -30.4
5.0 -50
Есть уравнение 0,14(180+х)=18+х
Шаг 1.
Раскроем скобки, т.е. умножим 0,14 на 180 и на х и сложим, получим
25,2+0,14х=18+-
Шаг 2.
Необходимо с одной стороны собрать буквы, с другой числа. Соберем буквы слева от знака равно, числа справа. Если переходите в другую сторону, знак меняется, был плюс икс справа, стал минус икс слева. Слева было 25,2 перешли вправо, изменили на -25,2. Все, что осталось на своих местах,знака не меняло.
0,14х-х=18-25,2
Как получили 0,86? чтобы сложить буквы, надо сложить коэффициенты, т.е. числа слева от букв и умножить на букву.
0,14х-х=х*(0,14-1)=-х(1-0,14)=-0,86х
здесь от единицы отнимали 14 сотых и получили 0, 86.
Шаг 3.
Посчитали правую и левую части. Получили
-0,86х=-7,2
Шаг 4.
Нашли неизвестный множитель. поделив на известный множитель произведение
х=-7,2/(-0,86)
Минус на минус дает плюс, умножили на сто числитель и знаменатель, чтобы получились целые числа.
х=720/86
Сократили,т.е. поделили и числитель и знаменатель на два. Получили
х= 360/43
Далее проверяли, жаль не видно в условии, какому интервалу принадлежит ли корень. Но это уже не столь важно. Как решать уравнение, детально рассказал.
См. Объяснение
Объяснение:
1) Числа 1000, 999, 998, 997, 996 и 995 не являются кратными 7, так как на 7 без остатка не делятся.
2) Число 994 делится на 7 без остатка:
994 : 7 = 142,
где 994 - делимое, кратное 7;
7 - делитель;
142 - частное, характеризующее кратность (столько раз число 7 повторилось в числе 994).
Таким образом, если число является кратным 7, то оно:
а) должно нацело делиться на 7 (994 : 7 = 142) - необходимое условие;
b) при делении на частное, характеризующее кратность (142), должно давать число, которому оно кратно (994 : 142 = 7) - достаточное условие.
3) Остальные числа, кратные 7:
987
980
973
966
959
952
945
938
931
924
917
910
903
896
889
882
875
868
861
854
847
840
833
826
819
812
805
798
791
784
777
770
763
756
749
742
735
728
721
714
707
700
693
686
679
672
665
658
651
644
637
630
623
616
609
602
595
588
581
574
567
560
553
546
539
532
525
518
511
504
497
490
483
476
469
462
455
448
441
434
427
420
413
406
399
392
385
378
371
364
357
350
343
336
329
322
315
308
301
294
287
280
273
266
259
252
245
238
231
224
217
210
203
196
189
182
175
168
161
154
147
140
133
126
119
112
105
98
91
84
77
70
63
56
49
42
35
28
21
14
7
4) Вопрос: является ли 0 кратным 7.
Для этого проверим 0 на соответствие необходимому и достаточному условиям:
а) 0 нацело делится на 7 (0 : 7 = 0), что удовлетворяет необходимому условию;
b) 0 при делении на частное, характеризующее кратность (0), не даёт число, которому он кратен 0 : 0 ≠ 7, так как на 0 делить нельзя, следовательно, число 0 не удовлетворяет достаточному условию, в силу чего не является числом, кратным 7.
5) Так как первое целое отрицательное число (-1) не кратно 7, то в диапазоне [-1; + 7] + 7 является наименьшим числом, кратным 7.
7
14
21
28
35
42
49
56
63
70
77
84
91
98
105
112
119
126
133
140
147
154
161
168
175
182
189
196
203
210
217
224
231
238
245
252
259
266
273
280
287
294
301
308
315
322
329
336
343
350
357
364
371
378
385
392
399
406
413
420
427
434
441
448
455
462
469
476
483
490
497
504
511
518
525
532
539
546
553
560
567
574
581
588
595
602
609
616
623
630
637
644
651
658
665
672
679
686
693
700
707
714
721
728
735
742
749
756
763
770
777
784
791
798
805
812
819
826
833
840
847
854
861
868
875
882
889
896
903
910
917
924
931
938
945
952
959
966
973
980
987
994