из условия задачи: 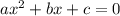
решим систему уравнений, где в одном поменяем a и b, а в другом b и c.
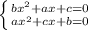
выразим дискриминант в обоих уравнениях и приравняем к 0, т.к. корень должен быть 1.
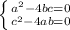
выразим 4b из первого уравнения и подставим во второе:
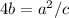
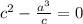
т.к. 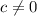
тогда 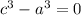
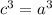

подставим в выражение, где твыразили 4b
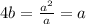
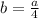
подставим все получившиеся коэффициенты в первое уравнеие:
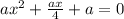
выразим дискриминант:
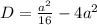
видно, что дискриминант получится отрицательным, следовательно у данного трехчлена решений нет.
ответ: корней нет
утром на поездку из А в Б фермер потратил 2 часа=120минут(8:00-6:00)
обратно затратил на дорогу из Б в А час 20 минут=1(1/3(одна целая одна 3)(14:00-12:40(потому что 12:30+отдых 10 минут)
Как я понимаю тебе нужно найти скорость)))
тогда обозначим скорость езды из А в Б - х
тогда скорость из Б в А получаем - х+9
состовляем уравнение
рассотяние из А в Б= 2х
рассотяние из Б в А =1(1/3)*(x+9)
так как расстояние одинаковое приравниваем их
2x=1(1/3)*(x+9)
домножим все уравнение на 3 что бы избавится от дробей
6х=4(х+9)
6х=4х+36
2х=36
х=18 км/ч-скорость из А в Б
18+9=27км/ч- скорость из Б в А
ответ:18 км/ч-скорость из А в Б; 27км/ч- скорость из Б в А
|a|=-a, если a<0
1) a<0 2|a|-|a-3| = 2(-a) -(-(a-3))=-2a+(a-3)= -a+a-3= -3
2) a<0 3a-3|a| = 3a -3(-a) = 3a+3a = 6a