
Наверное за это и не зачли правильный ответ .
В 3 пункте вы спутали с решением неполного квадратного уравнения.
Например, при решении уравнения х²=225 , обычно пишут х=+/- 15 . И это верно. Просто упускают запись: √х²=√225 ⇒ |x|=15 , пользуясь правилом, что √х²=|x| .
А из |x|=15 следует, что "х" может равняться либо 15, либо (-15) , то есть х=+/-15 , так как модуль положительного числа равен самому числу: |15|=15 , а модуль отрицательного числа равен числу, ему противоположному: |-15|=15 .
Фактически после записи х²=225 надо писать +/- х=15 , так как √225=15, а потом уже х=+/-15 .
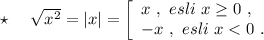
2a-1
10a^{2} -a-2
Мы знаем, что дробь равна нулю, когда числитель равен нулю, а знаменатель - нет.
10а^{2} -a-2\neq 0
Разложим знаменатель на множители, для того, чтобы увидеть: можно ли сократить дробь. А для того, чтобы разложить на множители, мы знаменатель приравняем к нулю и найдём корни квадратного уравнения.
10а^{2} -a-2=0
D=b^{2} -4ac
D=1-4*10*(-2)=1+80=81
\sqrt{D} = \sqrt{81} = 9
a_{1} = 1+9 = 10 = 1 = 0,5
2*10 20 2
a_{2} = 1-9 = -8 = -2 = -0,4
2*10 20 5
Разлаживаем на множители: 10*(a-0,5)(a+0,4).
Теперь подставляем разложеный на множители знаменатель в дробь, а в числителе выносим общий множитель 2 (чтобы мы смогли сократить дробь.
2*(a-0,5)
10*(a-0,5)(a+0,4)
Сокращаем дробь на множитель (a-0,5) - у нас остаётся 1, и на множитель 2 - в числителе останется 1. а в знаменателе 5. Получается:
1
5*(a+0,4)
да все правильно посчитал
угол AFB=90° это вроде далее какая-то теорема есть типа 2 биссектрисы по одну сторону от секущей образуют прямой угол
ну и доказал ты это правильно
ну а дальше по теореме Пифагора √(12²+9²)=15