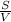, 
= 4 часа — время, потраченное легковой машиной на путь. 
График линейной функции является прямой линией, с чем и связано ее название. Это касается вещественной функции одной вещественной переменной.
Частный случай ~b=0 линейной функции называется однородными линейными функциями (это в сущности синоним прямой пропорциональности) , в отличие от b \neq 0 — неоднородных линейных функций.
y = kx + b(для функций одной переменной) .
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности.
f'(x)=2x-4
x^2-4x+4=2x-4
x^2-4x+4-2x+4=0
x^2-6x+8=0
D=36-32=4
x1=4
x2=2 эти точки верхняя и нижняя граница интеграла
интегал(2х-4-х^2+4х-4)dx|4 2=интеграл (-х^2+6х-8)dx |4 2 = -x^3/3+6x^2/2-8x|4 2= (-4^3/3+3×4^2-8×4-2^3/3-3×2^2+8×2=-64/3+48-32-8/3-12+16=-72+20=-52
|4 2 верхняя и нижняя граница интеграла