Question

Актуально до 16 часов сегодня 5 июня. Интегралы. $\int\limits {sinx*sin\frac{x}{2}*sin\frac{x}{3} } \, dx$
Максимально подробно.

Answer 1

$\sin( \alpha ) \times \sin( \beta ) = \frac{1}{2} ( \cos( \alpha - \beta ) - \cos( \alpha + \beta ) ) \\$

$\\\int\limits \sin(x) \sin( \frac{x}{2} ) \sin( \frac{x}{3} ) dx = \int\limits \frac{1}{2} ( \cos(x - \frac{x}{2} ) - \cos(x + \frac{x}{2} )) \times \sin( \frac{x}{3} ) dx = \\ = \frac{1}{2} \int\limits( \cos( \frac{x}{2} ) - \cos( \frac{3x}{2} ) ) \sin( \frac{x}{3} ) dx = \\ = \frac{1}{2} \int\limits \cos( \frac{x}{2} ) \sin( \frac{x}{3} ) dx - \frac{1}{2} \int\limits \cos( \frac{3x}{2} ) \sin( \frac{x}{3} ) dx$

$\\\sin( \alpha ) \times \cos( \beta ) = \frac{1}{2} ( \sin( \alpha + \beta ) + \sin( \alpha - \beta ) ) \\$

$\\1) \frac{1}{2} \int\limits \cos( \frac{x}{2} ) \sin( \frac{x}{3} ) dx = \\ = \frac{1}{4} \int\limits( \sin( \frac{x}{2} + \frac{x}{3} ) + \sin( \frac{x}{3} - \frac{x}{2} ) )dx = \\ = \frac{1}{4} \int\limits \sin( \frac{5x}{6} ) dx - \frac{1}{4} \int\limits \sin( \frac{x}{6} ) dx = \\ = \frac{1}{4} \times \frac{6}{5} \int\limits \sin( \frac{5x}{6} ) d( \frac{5x}{6} ) - \frac{1}{4} \times 6 \int\limits \sin( \frac{x}{6} ) d( \frac{x}{6} ) = \\ = - \frac{3}{10} \cos( \frac{5x}{6} ) + \frac{3}{2} \cos( \frac{x}{6} ) + c$

$\\2) \frac{1}{2} \int\limits \cos( \frac{3x}{2} ) \sin( \frac{x}{3} ) dx = \\ = \frac{1}{2} \times \frac{1}{2} \int\limits( \sin( \frac{3x}{2} + \frac{x}{3} ) + \sin( \frac{x}{3} - \frac{x}{2} )) dx = \\ = \frac{1}{4} \int\limits( \sin( \frac{11x}{6} ) - \sin( \frac{7x}{6} ) )dx = \\ = - \frac{1}{4} \times \frac{6}{11} \cos( \frac{11x}{6} ) + \frac{1}{4} \times \frac{6}{7} \cos( \frac{7x}{6} ) + c = \\ = - \frac{3}{22} \cos( \frac{11x}{6} ) + \frac{3}{14} \cos( \frac{7x}{6} ) + c$

$- \frac{3}{10} \cos( \frac{5x}{6} ) + \frac{3}{2} \cos( \frac{x}{6} ) + \frac{3}{22} \cos( \frac{11x}{6} ) - \frac{3}{14} \cos( \frac{7x}{6} ) + c \\$

Answer 2

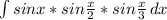
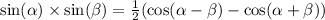
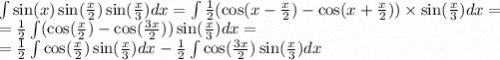
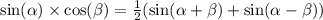
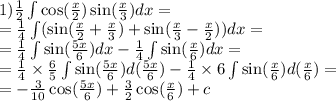
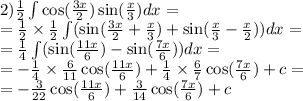
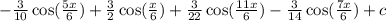
Объяснение:

sin(x/2)×sin(x/3)=(cos(x/2-x/3)-cos(x/2+x/3))/2=(cos(x/6)-cos(5x/6))/2

sinx×cos(x/6)=(sin(x-x/6)+sin(x+x/6))/2=(sin(5x/6)+sin(7x/6))/2

sinx×cos(5x/6)=(sin(x-5x/6)+sin(x+5x/6))/2=(sin(x/6)+sin(11x/6))/2

sinx×sin(x/2)×sin(x/3)=(sin(5x/6)+sin(7x/6))/4-(sin(5x/6)+sin(7x/6))/4=

(sin(5x/6)+sin(7x/6)-sin(5x/6)-sin(7x/6))/4