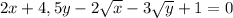 . Найдите tg α, где α - угол, образуемый вектором OM с положительным направлением оси OX.
. Найдите tg α, где α - угол, образуемый вектором OM с положительным направлением оси OX.
ответ: 4/9
Объяснение:
Из прямоугольного треугольника (рисунок):
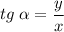
Следовательно, необходимо найти частное y/x.
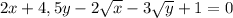
Соберём полные квадраты, добавив необходимое слагаемое. Для удобства можно провести замену u = √x, v = √y
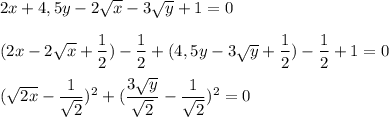
Сумма квадратов равна нулю, когда каждое слагаемое равно нулю:
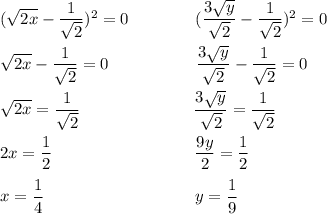
Тогда, имеем:
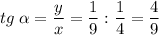
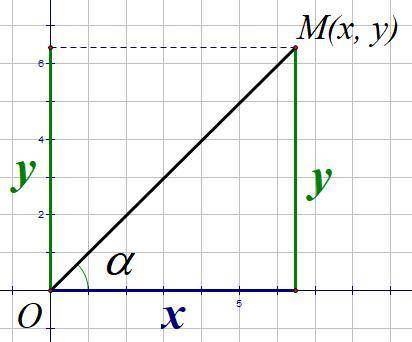
35 км/ч
Объяснение:
Дано:
S₁ = 35 км
S₂ = 34 км
t = 2 ч
Vр = 1 км/ч
V - ?
1)
Заметим, что собственная скорость лодки равна скорости ее движения по озеру:
V₁ = V
Время, затраченное на движение по озеру:
t₁ = S₁ / V₁
или
t₁ = S₁ / V.
2)
Время, затраченное на движение по реке.
Заметим, что река впадает в озеро, а это значит, что лодка двигалась против течения: V₂ = V - Vp
t₂ = S₂ / V₂ или
t₂ = S₂ / (V - Vp)
3)
Общее время движения:
t = t₁ + t₂
или
t = S₁ / V₁ + S₂ / (V - Vp)
Подставляем данные и решаем уравнение:
2 = 35 / V + 34 / (V - 1)
2·V·(V-1) = 35·(V-1) + 34·V
2·V² - 2·V = 35·V - 35 +34·V
2·V² - 71·V + 35 = 0
Решая это квадратное уравнение, получаем:
V = (71-69)/4 = 0,5 км/ч (слишком маленькая скорость...)
V = (71+69)/4 = 35 км/ч
4/9
Объяснение: