1) Вычислить площадь фигуры ограниченной линиями y=x+4 и осью ОХ и ОУ 2) Найти точку С на оси ОУ, равно-удаленную от точек А(6,-1) и В(-2,3) 3) Найти максимум и минимум функции y=x^4+8x^2+3
Точка М(2;1) - середина отрезка АВ . Проведём прямую через точку М перпендикулярно АВ . На этом перпендикуляре все точки будут равноудалены от концов отрезка АВ .
Чтобы найти координаты точки С на оси ОУ, найдём точку пересечения перпендикуляра с осью ОУ (х=0) .
Весь объем работы (заказ) = 1 Время на выполнение всего объёма работы: II рабочий х ч. I рабочий (х-4) ч. Производительность труда при работе самостоятельно: II рабочий 1/х объема работы в час I рабочий 1/(х-4) об.р./ч. Производительность труда при совместной работе: 1/х + 1/(х-4) = (х -4 +х) / (х(х-4)) = (2х-4)/ х(х-4) об.р./час Время работы 2 часа. Выполненный объем за 2 часа совместно : (2/1) * (2х -4) / х(х-4) = (4х-8)/(х (х-4)) Уравнение. (4х-8)/(х(х-4)) + 1/(х-4) = 1 (4х -8 +х) / (х(х-4)) = 1 знаменатель ≠ 0 ⇒ х≠0 ; х≠4 (5х-8)/ (х² - 4х) = 1 |*(x²-4x) 5x - 8 = x² -4x x² -4x -5x +8 =0 x² -9x +8 =0 D= (-9)² - 4*1*8 = 81 - 32 = 49 =7² D>0 - два корня уравнения х₁= (9 - 7) /(2*1) = 2/2 = 1 (ч.) противоречит условию задачи , т. к. в данном случае II рабочий может выполнить весь объем работы за час самостоятельно, а рабочие выполняли заказ совместно в течение 2-х часов , а потом I рабочий выполнял остаток заказа. х₂ =(9+7)/2 = 16/2 = 8 (ч.) время на выполнение всего объема работы II рабочим.
ответ: за 8 часов может выполнить всю работу второй рабочий.
Точка М(2;1) - середина отрезка АВ . Проведём прямую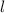 через точку М перпендикулярно АВ . На этом перпендикуляре все точки будут равноудалены от концов отрезка АВ .
через точку М перпендикулярно АВ . На этом перпендикуляре все точки будут равноудалены от концов отрезка АВ .
Чтобы найти координаты точки С на оси ОУ, найдём точку пересечения перпендикуляра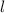 с осью ОУ (х=0) .
с осью ОУ (х=0) .