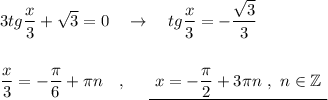
1-й
Пусть двухместных номеров х, тогда трехместных - (16 - х), в них разместились соответственно 2х и 3(16 - х) туристов. Т.к. туристов всего 42, то составим и решим уравнение
2х + 3(16 - х) = 42,
2х + 48 - 3х = 42,
-х = 42 - 48,
-х = -6,
х = 6.
Значит, двухместных номеров туристы заняли 6, а трехместных:
16 - 6 = 10 (ном.)
ответ: 6 номеров и 10 номеров.
2-й с системы)
Обозначим: х - количество двухместных номеров, y - количество трехместных номеров. По условию составим систему уравнений:
х + y = 16,
2x + 3y = 42.
Выразим из первого уравнения системы переменную х и подставим во второе уравнение:
x = 16 - y,
2(16 - y) + 3y = 42.
Решим получившееся уравнение:
2(16 - y) + 3y = 42,
32 - 2y + 3y = 42,
32 + у = 42,
y = 42 - 32,
у = 10.
Имеем: у = 10, тогда x = 16 - 10 = 6.
Значит, двухместных номеров туристы заняли 6, а трехместных - 10.
ответ: 6 и 10 номеров.