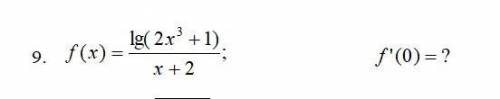
![f(x)=\dfrac{\lg(2x^{3}+1) }{x+2}\\\\f'(x)=\Big(\dfrac{\lg(2x^{3}+1) }{x+2}\Big)'=\dfrac{[\lg(2x^{3}+1)]' \cdot(x+2)-\lg(2x^{3}+1)\cdot(x+2)' }{(x+2)^{2} } =\\\\=\dfrac{\dfrac{1}{(2x^{3}+1)\cdot\ln10 }\cdot(2x^{3}+1)'\cdot(x+2)-\lg(2x^{3}+1)}{(x+2)^{2} }=\\\\=\dfrac{\dfrac{6x^{2} }{(2x^{3}+1)\cdot ln10}\cdot(x+2)-\lg(2x^{3} +1) }{(x+2)^{2} }=\dfrac{\dfrac{6x^{2}\cdot (x+2)}{(2x^{3}+1) ln10} -\lg(2x^{3}+1) }{(x+2)^{2} }](/tpl/images/2005/1458/98898.png)
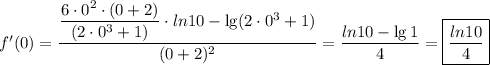
a)y(наиб)=2
y(наим)=-2
b)y(наим)=-29
y(наиб)=31
Объяснение:
a)
1)Находим производную функции :
f'(x)=3x^2-3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2-3=0 --> x=1
x=-1
3) Промежутку принадлежит только точка x=1 , поэтому значения функции на концах и в точке 1:
f(0)=0
f(1)=-2-наим
f(2)=8-6=2-наиб
б)
1)Находим производную функции :
f'(x)=3x^2+3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2+3=0 --> решений нет , значит наибольшее значение достигает правом конце отрезка [-3;3] , а наименьшее - в левом:
3) f(-3)=-27-3+1=-29
f(3)=27+3+1=31
Відповідь:
1) ні
в загальному випадку ні, треба що б прямі перетиналися
2) так
бо сторони трикутника перетинаються
3) не зрозуміле питання СB |(ВМС ), що треба довести? точка М лежить в площині АВС чи ні
4) МО перпендикулярна до АВС
у нас виходить піраміда в основі якої лежить прямокутник
якщо розглянути трикутники АМС і DМВ, то
- МО є медіаною, точка О ділить діагоналі порівну у прямокутника
-вони рівнобедрені, за умовою, тому МО є також і висотою, тому перпендикулярна АС та DВ, двом прямим, що перетинаються. Отже
МО перпендикулярна до АВС
Пояснення: