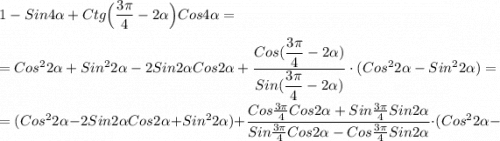
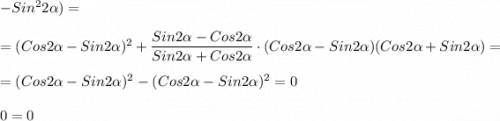
Тождество доказано
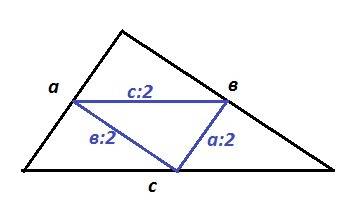
Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.
ответ: 0 = 0
Объяснение: преобразуем последний член выражения
= ((- 1 - сtg 3π/4 · ctg2α) / (ctg3π/4- ctg2α)) ·cos4α = /cgt3π/4= -1/ =
( -(1-ctg2α) / (1+ctg2α) )· cos4α = / ctg2α = cos2α/sin2α / =(- (sin2α-cos2α) / (sin2α + c0s2α) ) · (cos²2α - sin²2α) = - (cos2α - sin2α)² = -(1-2·sin2α·cos2α) =
sin4α -1
После подстановки в исходное тождество, получим: 1-sin4+sin4α-1 =0 ч. т. д.