Смотри решение.
Объяснение:
1. Запишем уравнение в исходном виде:
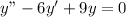
2. Запишем характеристическое уравнение:
λ^2 - 6λ + 9 = 0
3. Решаем его через дискриминант:
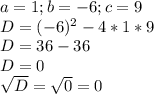
4. Находим λ:
λ_1 = λ_2 = 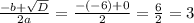
5. Записываем общее решение данного дифферинциального уравнения:
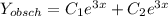
{-8*2+(-3)=-19 {-19=-19
(2;-3) является решением системы
Числа (-1;8)
{10*(-1)-3*8=29 <=> {-34=29
{-8*(-1)+8=-19
(-1;8) не является решением системы.
Числа (4;4)
{10*4-3*4=29 <=> {28=29
{-8*4+4=-19
(4;4) не является решением системы
Система 2.
б){-3x+y=11
{5x+y=3
Числа (2;-3)
P { margin-bottom: 0.21cm; }
{-3*2+(-3)=11 <=> {-9=11
{5*2+(-3)=3
(2;-3) не является решением системы
Числа (-1;8)
{-3*(-1)+8=11 <=> {11=11
{5*(-1)+8=3 {3=3
(-1;8) является решением системы
Числа (4;4)
{-3*4+4=11 <=> {-8=11
{5*4+4=3
(4;4) не является решением системы
Стандартный решения такого уравнения - с характеристического уравнения k²-6k+9=0; k=3 - кратный корень;
Однако в простых случаях ответ можно получить без всякой теории. В данном случае, домножив уравнение на можем записать его в виде
можем записать его в виде