Алгебра: F(x)=8x^7+4+x^5-7x f(x)=6x^4-3x^3+4x^2+3

1. Переносим все x и y в одну сторону Выражаем y: Подставляем в первое уравнение полученный у: Получаем квадратное уравнение: Решаем его: Подставляем полученное значение во второе уравнение: 2. Умножаем первое уравнение на 3: Вычитаем из первого уравнения второе: Подставляем полученное значение во второе уравнение: 3. Пусть первый комбайнер закончит уборку за x часов, а второй комбайнер - за x+4 часов. Тогда производительность первого комбайнера - , а производительность второго - . Общая производительность...

F(x)=8x^7+4+x^5-7x
f(x)=6x^4-3x^3+4x^2+3

👇

Увидеть ответ

Открыть все ответы

Ответ:

Ananasabricos

17.12.2021

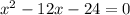
1) x^2 - 12x - 24 = 0

$D = 12^2 - 4\cdot (-24) = 144+4\cdot 24 0$

данное уравнение имеет два различных корня.

по теореме Виета:

x_1 + x_2 = 12

$x_1\cdot x_2 = -24$

Т.к. произведение корней отрицательно, то два корня разных знаков: меньший - отрицательный, больший - положительный.

2) 3x^2 - 12x + 4 = 0

$D = 12^2 - 4\cdot 3\cdot 4 = 144 - 4\cdot 12 =144 - 48 0$

уравнение имеет два различных корня.

по теореме Виета:

$x_1 + x_2 = \frac{12}{3} = 4$

$x_1\cdot x_2 = \frac{4}{3}$

Т.к. произведение корней положительно, то имеет два корня одного знака, а т.к. сумма корней положительна, то имеет два положительных корня.

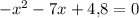
3) $-x^2 - 7x + 4{,}8 = 0$

$D = 7^2 - 4\cdot(-1)\cdot 4{,}8 = 49 + 4\cdot 4{,}8 0$

уравнение имеет два различных корня. По т. Виета:

$x_1 + x_2 = -\frac{-7}{-1} = -7$

$x_1\cdot x_2 = \frac{4{,}8}{-1} = -4{,}8$

Т.к. произведение корней отрицательно, то имеет два корня различных знаков: меньший - отрицательный, больший - положительный.

4) $-3x^2 + 2{,}2x + 9{,}24 = 0$

$D = 2{,}2^2 - 4\cdot(-3)\cdot 9{,}24 = 2{,}2^2 + 4\cdot 3\cdot 9{,}24 0$

уравнение имеет два различных корня. По т. Виета:

$x_1+x_2 = -\frac{2{,}2}{-3} = \frac{2{,}2}{3} 0$

$x_1\cdot x_2 = \frac{9{,}24}{-3} < 0$

Т.к. произведение корней отрицательно, то имеет два корня разных знаков: меньший - отрицательный, больший - положительный.

4,7(90 оценок)

Ответ:

Pipidastet

17.12.2021

1. $\left \{ {{xy+2=0} \atop 2x-y+4=0}} \right.$
Переносим все x и y в одну сторону
$\left \{ {{xy=-2} \atop {2x-y=-4}} \right.$
Выражаем y:
$\left \{ {{xy=-2} \atop {y=2x+4}} \right.$
Подставляем в первое уравнение полученный у:
$\left \{ {{x*(2x+4)=2} \atop {y=2x+4}} \right.$
Получаем квадратное уравнение:
$2x^{2} +4x+2=0$
Решаем его:
$D = b^{2} - 4 ac= 4^{2} - 4*2*2=16-16=0$
$x_{1,2} = \frac{-b}{2a} = \frac{-4}{2*2} = -1$
Подставляем полученное значение во второе уравнение:
$\left \{ {{x=-1} \atop {y=2x+4}} \right.$
$\left \{ {{x=-1} \atop {y=2*(-1)+4}} \right.$
$\left \{ {{x=-1} \atop {y=2}} \right.$
2. $\left \{ {{7x-3y=27} \atop {x+9y=-15} \right.$
Умножаем первое уравнение на 3:
$\left \{ {{21x-9y=81} \atop {x+9y=-15}} \right.$
Вычитаем из первого уравнения второе:
20x=96

Подставляем полученное значение во второе уравнение:
4,8+9y=-15

$\left \{ {{x=4,8} \atop {y=-2,2}} \right.$
3. Пусть первый комбайнер закончит уборку за x часов, а второй комбайнер - за x+4 часов. Тогда производительность первого комбайнера - $\frac{1}{x}$ , а производительность второго - $\frac{1}{x+4}$ . Общая производительность двух комбайнеров $\frac{1}{x} + \frac{1}{x+4}$ или $\frac{1}{4,8}$
Решим уравнение:
$\frac{1}{x} + \frac{1}{x+4} = \frac{1}{4,8}$
Приводим к общему знаменателю:
$\frac{- x^{2} +5,6x+19,2}{4,8x(x+4)} =0$
Решаем квадратное уравнение:
$D=b^{2} -4ac=5,6 ^{2} -4*(-1)*19,2=31,36+76,8=108,16$
$x_{1} = \frac{-5,6+10,4}{2*(-1)} =-2,4$ - не удовлетворяет смыслу задачи
$x_{2} = \frac{-5,6-10,4}{2*(-1)} = 8$
8 часов потребуется первому комбайнеру
8+4=12