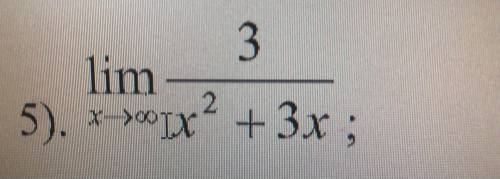
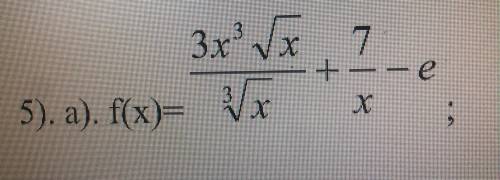
![1)\ \ \lim\limits _{x \to \infty}\dfrac{3}{x^2+3x}=\Big[\dfrac{3}{\infty }\Big]=0\\\\\\2)\ \ f(x)=\dfrac{3x^3\cdot \sqrt{x}}{\sqrt[3]{x}}+\dfrac{7}{x}-e\ \ \Rightarrow \ \ \ f(x)=3x^{\frac{19}{6}}+\dfrac{7}{x}-e}\\\\\\f'(x)=\dfrac{19}{6}\cdot x^{\frac{13}{6}}-\dfrac{7}{x^2}=\dfrac{19}{6}\cdot \sqrt[6]{x^{13}}-\dfrac{7}{x^2}](/tpl/images/2006/7105/a5e76.png)
1) sin x = √2/2
x = (-1)ⁿ × arcsin √2/2 + πn, n∈Z
x = (-1)ⁿ × π/4 + πn, n∈Z
2) sin x = -√2/2
x = (-1)ⁿ × arcsin (-√2/2) + πn, n∈Z
x = (-1)ⁿ × -arcsin √2/2 + πn, n∈Z
x = (-1)ⁿ × (-π/4) + πn, n∈Z
3) sin x = -√3/2
x = (-1)ⁿ × arcsin (-√3/2) + πn, n∈Z
x = (-1)ⁿ × -arcsin √3/2 + πn, n∈Z
x = (-1)ⁿ × (-π/3) + πn, n∈Z
4) sin x = √3/2
x = (-1)ⁿ × arcsin √3/2 + πn, n∈Z
x = (-1)ⁿ × arcsin √3/2 + πn, n∈Z
x = (-1)ⁿ × π/3 + πn, n∈Z
5) sin x = 4/5
x = (-1)ⁿ × arcsin 4/5 + πn, n∈Z
x = (-1)ⁿ × 0,927295 + πn, n∈Z
x = (-1)ⁿ × 53,1° + πn, n∈Z
0.3 м на 0.2 м это 30 см на 20 см
если начнет выкладывать вдоль длинной 30 см стороны , то получит 30/3 = 10 наклеек
и 6 рядов наклеек вверх до 18 см итого
6*10 = 60 наклеек
а полоса 2 на 30 ничем не наклеится
также, если начнет выкладывать вдоль короткой 20см стороны, получит 6 наклеек и вверх на 30 см еще 10 рядов
итого 6*10 = 60
хотя если посчитать площадь 30*20 = 600 и поделить на 3*3 = 9 получим 66 штук
Только не стоит забывать, что наклейки 3 на 3 не режутся и за края не выходят, только целиком на площадь картона
ответ 60