вполне вероятно, что я могла и не правильно решить задание, но я думаю так*
я думаю тут просто вместо N надо подставить числа 1-6
б)
X1 = 1^2 +1 = 2
X2 = 2^2 + 1 = 5
X3 = 3^2 + 1 = 10
X4 = 4^2 + 1 = 17
X5 = 5^2 + 1 = 26
X6 = 6^2 + 1 = 37
г)
X1 = (-1)^(1+1) * 2 = 2
X2 = (-1)^(2+1) * 2 = -2
X3 = (-1)^(3+1) * 2 = 2
X4 = (-1)^(4+1) * 2 = -2
X5 = (-1)^(5+1) * 2 = 2
X6 = (-1)^(6+1) * 2 = -2
е)
X1 = 0,5*4^1 = 2
X2 = 0,5*4^2 = 8
X3 = 0,5*4^3 = 32
X4 = 0,5*4^4 = 128
X5 = 0,5*4^5 = 512
X6 = 0,5*4^6 = 2048
Но что то мне подсказывает, что это прогрессии. АП и ГП. Я их терпеть не могу. 1 раз как так и забыли. Но для решения таких заданий - они еобходимы. Этот тут повезло что числа лёгкие. А если бы надо было первые 20 чисел? все высчитывать что ли?... Надо мне повторить прогрессии...
Произведение чисел, переменных и их степеней называется одночленом, например,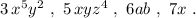 
Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
,
.
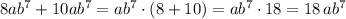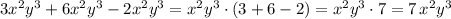Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
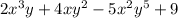не может быть упрощена, так как буквенные части одночленов различны.
А вот пример, где можно немного упростить сумму одночленов, но в результате всё равно получим многочлен:
.
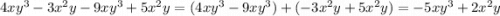Множества корней уравнений не совпадают, значит они не равносильны.