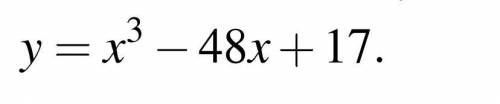
раскроем скобки,
y=x^2+10x+25(x+6)-8
y=x^3+10x^2+25x+6x^2+60x+150-8
y=x^3+16x^2+85x-142
находим производную
y=3x^2+32x+85
3x^2+32x+85=0
находим X через дискрименант D=b^2-4ac=1024-1020=4 ,корент из 4 равен 2
X(1,2)=-b(+)(-) D/2a=x(1)=-17/3=-5,6
x(2)=-5
нам нужно найти наименьшее значение функции т.е.Y
подстовляем найденные X в Функцию
y(1)=(-5,6+5)^2*(x+6)-8=-7,8
y(2)=(-5+5)^2*(x+6)-8=-8
делаем вывод что из промежутка [-5,5;1]наименьшее значение принимает при -5,5
ОТВЕТ:-5.5
у=(х-5)²·(х-3)+ 10
y' = 2·(х-5)·(х-3) + (х-5)²
ищем минимум
2·(х-5)·(х-3) + (х-5)² = 0
(х-5)·(2х - 6 + х - 5) = 0
(х-5)·(3х - 11) = 0
х₁ = 5, х₂ = 11/3 = 3 2/3
Исследуем знак производной в интервалах
+ - +
11/3 5
У'(3) = -2·(-2) = 4 > 0 y возрастает
У'(4) = -1·1 = -1 < 0 y убывает
У'(6) = 1·7 = 7 > 0 y возрастает
Точка минимума х₁ = 5
У min = у(5) = (5-5)²·(5-3)+ 10 = 0·2 + 10 = 10
На промежутке от 4 до 8 функция ведёт себя так:убывает при х∈[4 ; 5] и возрастает при ∈[5 ; 8].
Следовательно, наименьшее значение функции совпадает с её минимальным значением
ответ: у наим = 10
Объяснение:
Смотрите решение на фотографии