формула производной произведения на фото
у=(х²+х)(2х-4)
у'=(2х+1)(2х-4)+2(х²+х)=4х²-8х+2х-4+2х²+2х=6х²-4х-4
у'(0)=6*0-4*0-4=-4
у'(2)=6*4-4*2-4=24-8-4=12
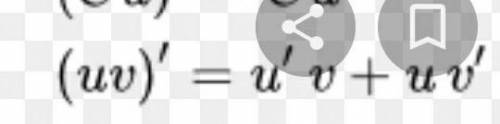
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
y = (x² + x)(2x – 4) = 2x³ – 4x² +2x² – 4x = 2x³ – 2x² – 4x
y' = 6x² – 4x – 4
y'(0) = 6·0² – 4·0 – 4 = –4
y'(2) = 6·2² – 4·2 – 4 = 12