так как мы не можем определить нули производной, значит функция не имеет стационарных точек. Подставив любое значение из области определения функции( D(y): x є (4 ; ∞) ) мы увидим что , а это сведетельствует что она монотонно возростает на всем промежутке на котором определена
Раз по реке она шла меньше времени при большем расстоянии, значит явно шла по течению. Пусть её собственная скорость V, время пути по реке t, тогда верны следующие соотношения(не забудем перевести минуты в часы): 36 = (V+2)*t, 35 = V * (t+1/20) Раскрываем скобки: 36 = Vt+2t 35=Vt+V/20 Вычитаем из второго уравнения первое: 1 = V/20 - 2t Выражаем скорость: V/20 = 1 + 2t V = 20 + 40 t Подставим это соотношение, например, в первое уравнение: 36=(20+40t+2)t 36 = 40 t^2 + 22 t 40 t^2 + 22 t - 36 = 0 Сокращаем: 20 t ^2 + 11 t - 18 = 0 Решаем квадратное уравнение: D = 11*11 + 4 *20*18 = 121 + 1440 = 1561 = 39,5 (округлённо) t = (-11+-(39,5)) / 40 = {-1,25; 0,7} Время отрицательным быть не может, единственный подходящий результат - 0,7 ч. Подставляем в полученное выражение скорости: V = 20 + 40 t = 20 + 40 * 0,7 = 48 км/ч. Хотя явно не очень сходится, даже со всеми округлениями. Возможно, в вычислениях ошибся, но ход решения примерно такой.
Решение Половина пути для второго автомобиля 0,5. Пусть х км/ч – скорость первого автомобилиста, тогда (х + 54) км/ч - скорость второго автомобилиста Время второго автомобиля, за которое он весь путь 0,5 / 36 + 0,5/(x + 54) Время первого автомобиля равно времени второго автомобиля. 1/x = 0,5 / 36 + 0,5/(x + 54) 1/x - 0,5 / 36 - 0,5/(x + 54) = 0 36(x + 54) – 0,5x(x + 54) – 0,5*36x = 0 36x + 1944 – 0,5x² - 27x – 18x = 0 – 0,5x² - 9x + 1944 = 0 I : (-0.5) x² + 18x – 3888 = 0 D = 324 + 4*1*3888 = 15876 = 1262 X₁ = (- 18 – 126)/2 = - 72 не удовлетворяет условию задачи X₂ = (- 18 + 126)/2 = 54 54 км/ч - скорость первого автомобилиста ответ: 54 км/ч
![f(x)=\sqrt[]{x-4}+7](/tpl/images/4511/2984/20246.png)
нахождения экстремума.
Объяснение:
Найдем прозводную функции f(x):
найдем нули производной
так как мы не можем определить нули производной, значит функция не имеет стационарных точек. Подставив любое значение из области определения функции( D(y): x є (4 ; ∞) ) мы увидим что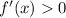
, а это сведетельствует что она монотонно возростает на всем промежутке на котором определена