Question

Высота, проведённая из вершины прямого угла, равна 2 см и делит гипотенузу на отрезки, один из которых больше другого на 3 см. Найдите стороны треугольника.

Answer 1

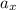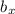Так как высота проведена из вершины прямого угла то высота попадет на гипотенузу.  А отрезки на которые делит высота гипотенузу являются проекциями катетов пусть  с-это гипотенуза  ; $\displaystyle\ a_x$  и   $\displaystyle\ b_x$   -это проекции катетов(сторон треугольников) a и b ;  для них есть правила  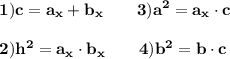                                                                                           $\displaystyle\bf 1)c=a_x+b_x\qquad 3)a^2=a_x\cdot c\\\\2)h^2=a_x\cdot b_x \qquad 4)b^2=b\cdot c$                                                                              нам известно    что  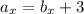 $\displaystyle\ a_x=b_x+3$     дальше будем использовать 2-ю формулу  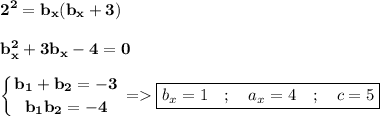                                                                                               $\displaystyle\bf 2^2=b_x(b_x+3)\\\\b_x^2+3b_x-4=0 \\\\\left \{ {{b_1+b_2=-3} \atop {b_1b_2=-4}} \right. =\boxed{b_x=1\quad ; \quad a_x=4\quad ; \quad c=5}$                                             Дальше найдем стороны a и b через 3-ю и 4-ю формулу  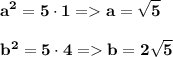                     $\displaystyle\bf a^2=5\cdot1= a=\sqrt{5} \\\\b^2=5\cdot4= b=2\sqrt{5}$                                                                                       ответ: у треугольника длины сторон равны   √5 ; 2√5  и 5