Заметим, что для любого корня уравнения вне зависимости от значения параметра произведение будет больше или равно 4.
Причем , если - корень уравнения. Но это невозможно, так как при имеем (неверно) при любом значении параметра.
Тогда , то есть условие ОДЗ будет выполнятся всегда.
Исходное уравнение будет иметь ровно один корень, либо если имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
Рассмотрим первый случай. Он достижим, когда .
При уравнение имеет корень , поэтому такое значение параметра не подходит.
При уравнение имеет корень , поэтому такое значение параметра подходит.
Рассмотрим второй случай. Он достижим, когда .
Здесь также важно, чтобы уравнение либо имело один корень , а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
Обратимся к первой ситуации:
В этом случае уравнение имеет корни или , первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
Для того чтобы вторая ситуация могла быть достижимой, необходимо, но не достаточно, чтобы выполнялось условие при . Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
Итого при или исходное уравнение имеет единственное решение.
Для того чтобы решать такие уравнения, сначала необходимо найти ОДЗ (область допустимым значений), или те корни, которые обращают знаменатель дроби в нуль. ОДЗ: Дальше, чтобы избавиться от знаменателя, нужно привести дроби к общему знаменателю и умножить на него обе части уравнения: Меняем знак второй дроби, чтобы у нас получилась формула сокращенного умножения, а вследствие и общий знаменатель, и умножаем на него. Решив его по т. Виета путем подбора, получим корни Возвращаемся к ОДЗ и видим, что 2 - посторонний корень, поэтому исключаем его и записываем в ответ -5. ответ: -5
3) f(x)= 1. Сначала находим область определения этой функции. Функция задана многочленом, D(f)=R , ну или (-∞;+∞) 2. Находим производную. Применяем формулы (2*²=4x) и x=1 (4*x=4*1=4) Итак: f '(x)=4x-4 3. Приравниваем полученную производную к нулю. f '(x)=0, 4x-4=0, решаем уравнение. 4x=4 x=1 ---⁻---(1)---⁺--- проверка знаков: проверим (+). Подставляем в полученную производную, например, цифру 2 вместо x: 4*2-4=4, число положительное, значит ставим знак плюс. Проверим (-). Подставим -1, -4-4=-8, число отрицательное, значит в интервале минус. Когда минус переходит на плюс, это считается точкой минимума. Наоборот - максимума. У нас минимум. xmin=1
(см. объяснение)
Объяснение:
ОДЗ:
Заметим, что для любого корня уравнения вне зависимости от значения параметра произведение
произведение 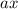 будет больше или равно 4.
будет больше или равно 4.
Причем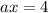 , если
, если 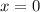 - корень уравнения. Но это невозможно, так как при
- корень уравнения. Но это невозможно, так как при 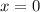 имеем
имеем 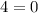 (неверно) при любом значении параметра.
(неверно) при любом значении параметра.
Тогда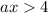 , то есть условие ОДЗ
, то есть условие ОДЗ  будет выполнятся всегда.
будет выполнятся всегда.
Исходное уравнение будет иметь ровно один корень, либо если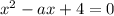 имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
имеет один корень, удовлетворяющий ОДЗ, либо если это уравнение имеет два корня, только один из которых удовлетворяет ОДЗ.
Рассмотрим первый случай. Он достижим, когда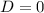 .
.
При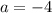 уравнение имеет корень
уравнение имеет корень  , поэтому такое значение параметра не подходит.
, поэтому такое значение параметра не подходит.
При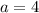 уравнение имеет корень
уравнение имеет корень 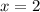 , поэтому такое значение параметра подходит.
, поэтому такое значение параметра подходит.
Рассмотрим второй случай. Он достижим, когда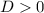 .
.
Здесь также важно, чтобы уравнение либо имело один корень , а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
, а другой положительный, либо один корень неположительный, а другой положительный, не равный единице.
Обратимся к первой ситуации:
В этом случае уравнение имеет корни или
или 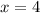 , первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
, первый из которых, отпадая, обеспечивает наличие единственного корня у исходного уравнения. Тогда такое значение параметра подходит.
Для того чтобы вторая ситуация могла быть достижимой, необходимо, но не достаточно, чтобы выполнялось условие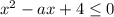 при
при 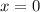 . Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
. Однако это невозможно, поэтому такой вариант рассматривать дальше не будем.
Итого при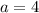 или
или  исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Задание выполнено!