Даны числа Найти x, при которых функция принимает наименьшее значение. Если для произвольного N решить трудно, рассмотрите случаи N=1, 2, 3, 4, 5, 2021, 2022. Ес ли для произвольных чисел решить трудно, возьмите в качестве k-го числа к-е простое число (напоминаю. что 1 не является простым числом). То есть
N=1: модуль не может принимать значения, меньшие 0. При этом - а значит и есть оптимальное [будем называть оптимальными искомые значения переменной] значение.
N=2: Тут возможны 3 случая.
1)
Тогда
2)
Тогда
3)
Тогда
Значит, оптимальными будут все значения .
N=2k:
Тогда функция представима в виде .
Для первого слагаемого оптимальными будут (как показано ранее) все точки отрезка .
Для второго слагаемого оптимальными будут все точки отрезка . При этом, по условию, имеем - то есть все точки этого отрезка оптимальны и для первого слагаемого
...
Для k-ого слагаемого оптимальными будут все точки отрезка . При этом - то есть все точки этого отрезка оптимальны и для остальных слагаемых. Но тогда все точки этого отрезка являются оптимальными для всего набора .
N=2k+1:
Тогда функция представима в виде
.
Проведя k шагов аналогичных рассуждений, получим, что для набора оптимален отрезок .
Для , как показано ранее, оптимально значение . При этом - то есть это значение оптимально и для остальных слагаемых. Но тогда оно оптимально для всего набора .
_____________________
Собственно, если N четно, ответом будет , а если нечетно,
А вот тут кроется подвох, ведь угол может быть задан в градусах, радианах, градах, минутах или секундах... Поскольку, при рассмотрении тригонометрических функций в математическом анализе всегда считается, что аргумент выражен в радианах, что упрощает запись; при этом само обозначение рад (rad) часто опускается, и тогда, при расчёте в радианах: A = cos0rad * tg45rad + 8 sin30rad = 1 * 1.6197751905 + 8 * (-0.9880316241) = −6,284477802; B = sin π/2 * ctg п/2 + 10 сos п/3 = 1 * 0 + 10 * 0,5 = 6; А + В = −6,284477802 + 6 = −0,284477802. При расчёте в градусах картина меняется: A = cos0° * tg45° + 8 sin30° = 1 * 1 + 8 * 0,5 = 5; B = sin π/2 * ctg π/2 + 10 сos π/3 = 0.027412133592 * 36.4664871307475277 + 10 * 0.999832979459 = 10,997954011; А + В = 5 + 10,997954011 = 15,997954011. Автору вопроса остаётся только определиться, в какой системе он желает получить ответ.
Если N четно,![x\in\left[a_\frac{N}{2};a_{\frac{N}{2}+1}\right]](/tpl/images/2009/1275/842d3.png) , а если нечетно,
, а если нечетно, 
Объяснение:
N=1: модуль не может принимать значения, меньшие 0. При этом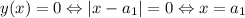 - а значит
- а значит 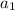 и есть оптимальное [будем называть оптимальными искомые значения переменной] значение.
и есть оптимальное [будем называть оптимальными искомые значения переменной] значение.
N=2: Тут возможны 3 случая.
1)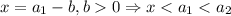
Тогда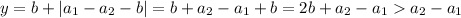
2)
Тогда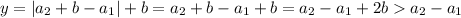
3)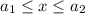
Тогда
Значит, оптимальными будут все значения![x\in [a_1;a_2]](/tpl/images/2009/1275/b38e6.png) .
.
N=2k:
Тогда функция представима в виде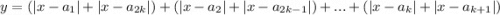 .
.
Для первого слагаемого оптимальными будут (как показано ранее) все точки отрезка![[a_1;a_{2k}]](/tpl/images/2009/1275/19eda.png) .
.
Для второго слагаемого оптимальными будут все точки отрезка![[a_2;a_{2k-1}]](/tpl/images/2009/1275/70f36.png) . При этом, по условию, имеем
. При этом, по условию, имеем ![[a_2;a_{2k-1}]\subset [a_1;a_{2k}]](/tpl/images/2009/1275/9e7a1.png) - то есть все точки этого отрезка оптимальны и для первого слагаемого
- то есть все точки этого отрезка оптимальны и для первого слагаемого
...
Для k-ого слагаемого оптимальными будут все точки отрезка![[a_k;a_{k+1}]](/tpl/images/2009/1275/a6e74.png) . При этом
. При этом ![[a_k;a_{k+1}]\subset [a_{k-1};a_{k+2}]\subset...\subset [a_1;a_{2k}]](/tpl/images/2009/1275/56cff.png) - то есть все точки этого отрезка оптимальны и для остальных слагаемых. Но тогда все точки этого отрезка являются оптимальными для всего набора
- то есть все точки этого отрезка оптимальны и для остальных слагаемых. Но тогда все точки этого отрезка являются оптимальными для всего набора 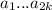 .
.
N=2k+1:
Тогда функция представима в виде
Проведя k шагов аналогичных рассуждений, получим, что для набора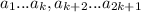 оптимален отрезок
оптимален отрезок ![[a_k;a_{k+2}]](/tpl/images/2009/1275/fe0a8.png) .
.
Для , как показано ранее, оптимально значение
, как показано ранее, оптимально значение 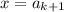 . При этом
. При этом ![a_{k+1}\in[a_k;a_{k+2}]](/tpl/images/2009/1275/94b66.png) - то есть это значение оптимально и для остальных слагаемых. Но тогда оно оптимально для всего набора
- то есть это значение оптимально и для остальных слагаемых. Но тогда оно оптимально для всего набора 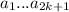 .
.
_____________________
Собственно, если N четно, ответом будет![\left[a_\frac{N}{2};a_{\frac{N}{2}+1}\right]](/tpl/images/2009/1275/77b21.png) , а если нечетно,
, а если нечетно, 