1 cлучай: a и b одинаковых знаков ab>=0 Воспользуемся неравенством: о средних (x+y)/2>=√xy |ab|=ab<=(a^2+b^2)/2=1/2 2ab<=1 Преобразуем: (a+b)^2-2ab=1 (a+b)^2=1+2ab<=2 Откуда |a+b|<√2 -√2<=a+b<=√2 ЧТД 2 cлучай: a и b разных знаков. Тут уже поинтересней: имеем: a^2=1-b^2<=1 тк b^2>0 |a|<=1 Анологично |b|<=1 тк одно положительное другое отрицательное,то можно сделать оценку: 0 <=a<=1 -1<=b<=0 Сложим эти сравнения: -1<=a+b<=1 А значит и верно что -√2<a+b<√2 что удовлетворяет рамкам неравенства. тк √2>1 чтд Заметим что равенство выполняется когда a=b=+-1/2
Объяснение:
1)
Применим правило Лопиталя:
Возвращаясь к исходному пределу, получим:
2)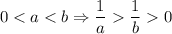
Тогда, согласно пункту 1,
Но тогда
С другой стороны, в исходном интеграле можно провести замену:
Значит,