В решении.
Объяснение:
Дана функция y=√x
а) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
у=√х
1) А(63; 3√7)
3√7 = √63
3√7 = √9*7
3√7 = 3√7, проходит.
2) В(49; -7)
-7 = ±√49
-7 = -7, проходит.
3) С(0,09; 0,3)
0,3 = √0,09
0,3 = 0,3, проходит.
б) х ∈ [0; 25]
y=√0 = 0;
y=√25 = 5;
При х ∈ [0; 25] у∈ [0; 5].
в) Найдите значения аргумента, если у∈ [9; 17]
у = √х
9=√х х=9² х=81;
17=√х х=17² х=289.
При х ∈ [81; 289] у∈ [9; 17].
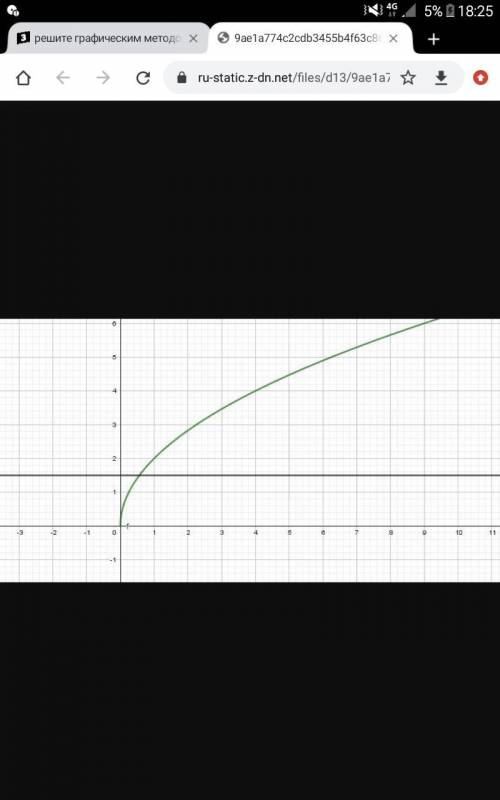
1) Построим графики функций и прямую параллельную оси ОХ
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
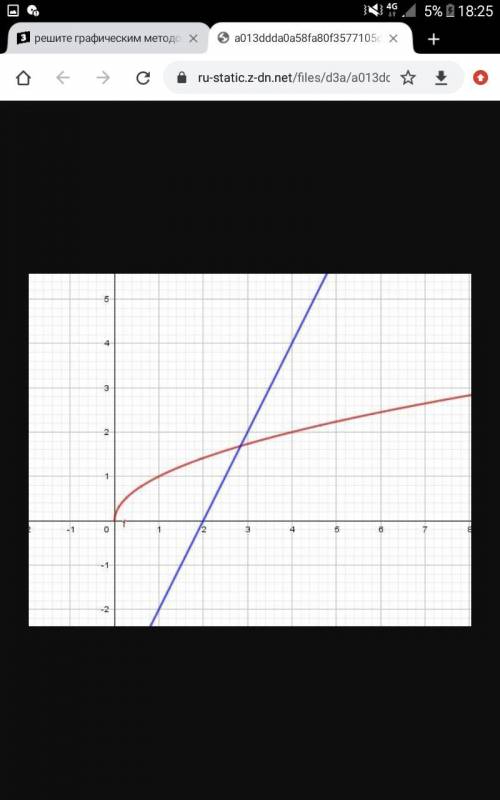
2) Построим график функции и прямую проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков
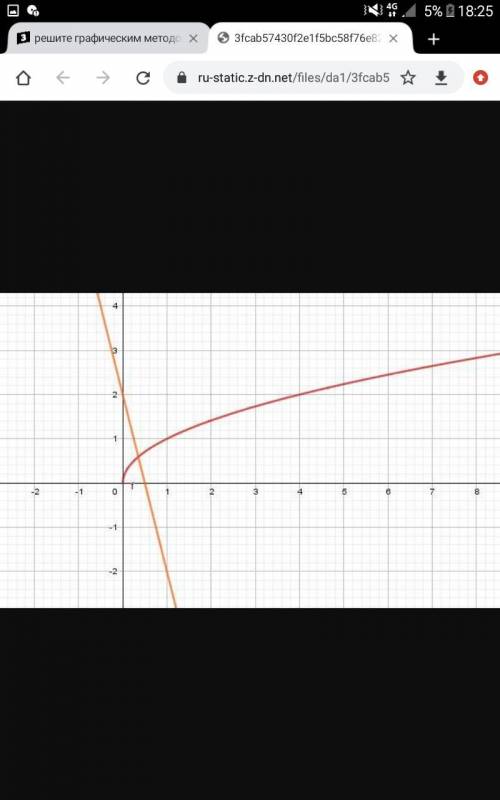
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна
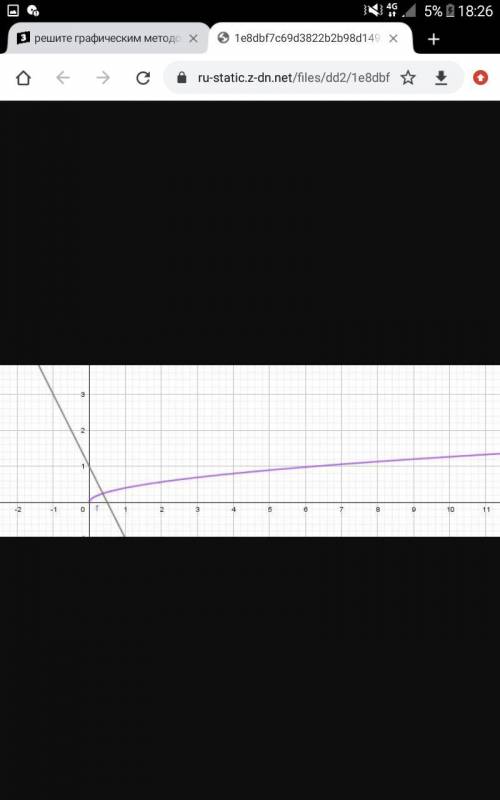
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна
Пусть :
x (га) − за день вспахивал первый тракторист;
y (га) − за день вспахивал второй тракторист.
Первый тракторист работал 8 дней, а второй тракторист - 5 дней , значит первый тракторист за 8 дней вспахал 8x (га) , а второй зa 5 дней вспахал
5y (га) . Работая вместе они вспахали 630 га . Составим первое уравнение :
8x + 5y = 630
За 3 дня первый тракторист вспахал 3x (га) , а второй за 4 дня вспахал
4y (га) . Составим второе уравнение :
4y - 3x = 34
Составим и решим систему уравнений :
ответ : первый тракторист вспахал за день 50 га , а второй 46 га .