
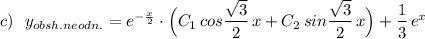
Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
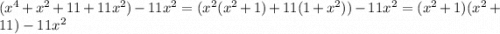
нельзя выносить множитель только из двух слагаемых имея при этом третье, поэтому мы можем добавить слагаемое и вычесть его за скобками, в данном случае нам удобно добавить 11х^2 потому что при вынесении общего множителя за скобку он даст нам такую же скобку как и первые два множителя, которую мы тоже потом вынесем.
Как понять какое слагаемое нужно добавить?
возьмем 2 слагаемых из которых мы можем вынести общий множитель
х^4 и х^2
выносим общий множитель х^2
х^2(х^2 +1)
получаем скобку (х^2 +1)
теперь нужно подумать, какое слагаемое нужно добавить, чтобы при вынесении общего множителя скобка была такой же, и это 11х^2 потому что при делении на 11 мы получим х^2 от нового слагаемого и 1 от уже имеющегося.
Если будут вопросы отвечу в комментариях