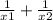
Длина сада 175 м
Ширина сада 140 м
Объяснение:
х - длина сада
у - ширина сада
2,45 га = 24500 (м кв)
По условию задачи периметр сада 630 метров
Система уравнений:
2(х+у)=630
х*у=24500
Во втором уравнении выразим х через у и подставим выражение в первое уравнение:
х=24500/у
2(24500/у)+2у=630
49000/у+2у=630
Избавляемся от дробного выражения, умножаем все части уравнения на у:
49000+2у²=630у
2у²-630у+49000=0/2 делим на 2 для удобства вычислений:
у²-315у+24500=0, квадратное уравнение, ищем корни:
у₁,₂=(315±√99225-98000)/2
у₁,₂=(315±√1225)/2
у₁,₂=(315±35)/2
у₁=140 х₁=24500/140=175
у₂=175 у₂=24500/175=140
Так как по условию х - длина участка, а у - ширина,
решение системы уравнений х=175
у=140
Проверка:
175 * 140 = 24500 (м кв)= 2,45 га
2*(175+140)=630 (м) изгородь сада, периметр. Всё верно.
Объяснение:
Пусть прямая задается уравнением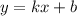
Поскольку прямая проходит через точку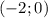 , то подставив её координаты в уравнение прямой получим:
, то подставив её координаты в уравнение прямой получим: 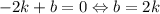
Значит наша прямая имеет вид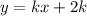
В точках пересечения значения функций должны быть равными
По т. Виета: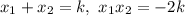 , значит
, значит
P.S.: Тут хорошо бы еще отметить, что поскольку в условии заранее известно, что прямая пересекает параболу в двух точках, то проверять условие наличия корней у квадратного уравнения не требуется. Так же, в последней строчке решения, при сокращении дроби на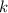 по идее необходимо убедиться что
по идее необходимо убедиться что 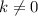 , однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)
, однако в этом случае точка пересечения будет только одна, поэтому подобные сокращение можно смело называть легальным)