Объяснение:
1) Если по условию задачи кубик подбрасывается один раз и надо найти вероятность того, что выпадет 2,3 или 5, то число благоприятных исходов равно 3.
m = 3
Число равновозможных исходов - 6.
n = 6
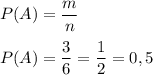
ответ: 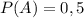
2) Если по условию задачи кубик подбрасывается три раза и надо найти вероятность того, что выпадут 2, 3, 5, то будем рассматривать независимые события.
Событие А = {выпала 2};
событие В = {выпала 3};
событие С = {выпала 5}.

P(ABC) = P(A) · P(B) · P(C)
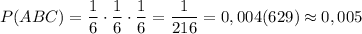
ответ: 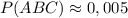
силий Тёркин»? Назовите подзаголовок поэмы. 3. Почему поэт пишет, что «на войне сюжета нету» и что книга «без начала и конца»? 4. Во для анализа главы «Переправа»: а) На какие части разделяют главу слова «Переправа, переправа...»? Каким настроением проникнута каждая часть главы? С какой интонацией следует читать эти строки? б) Что является «лейтмотивом» данной главы? Почему? в) Каким в этой главе предстаёт перед читателем Василий Тёркин? 5. Во для анализа главы «О награде»: а) Как построена эта глава? Дайте характеристику частей этой главы? б) Как проявляется здесь стилевое многообразие поэмы? в) Что нового об образе Тёркина мы узнаём в этой главе? г) Можем ли сказать, что автор сроднился с Тёркиным? В чём это проявляется? Что значит слово «родина» для каждого из них? е) Выделите в главе строки, которые являются рефреном произведения. Как вы думаете, почему именно такой рефрен включён Твардо
Объяснение:
Дробь не имеет смысла если её знаменатель равен нулю т.к. на ноль делить нельзя.
\dfrac{x}{x-4} ;\; x-4=0;\; \bold{x=4} dfrac{2b^2-9}{b(b-5)} ;\; b(b-5)=0;\; \bold{b=\{0;5\}}.
Дробь равна нулю если числитель равен нулю, а знаменатель - не равен.
\dfrac{x+1}{x} =0;\; \begin{Bmatrix}x+1=0\\x\ne 0\end{matrix} \\\begin{Bmatrix}x=-1\\x\ne 0\end{matrix} \qquad \bold{x=-1}dfrac{x(x-2)^2 }{x-2} =0;\; \begin{Bmatrix}x(x-2)^2 =0\\x-2\ne 0\end{matrix} \\\begin{Bmatrix}x=\{0;2\}\\x\ne 2\end{matrix} \qquad \bold{x=0}.
Объяснение:
удачи получить хорошую отметку
Объяснение:
Поскольку события не зависимые, то по теории вероятностей (правило произведения):
P = (1/6)·(1/6)·(1/6) = 1 / 6³ ≈ 0,005