Доказательство:
Дана последовательность
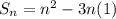
Допустим, что эта последовательность арифметическая прогрессия, тогда
при n = 1 получаем

при n = 2

и
а₂ = -2 - а₁ = -2 + 2 = 0
Таким образом разность арифметической прогрессии
d = a₂ - a₁ = 0 + 2 = 2
По известной формуле найдем n-й член арифметической прогрессии
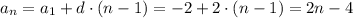
Известно, что сумма n членов арифметической прогрессии
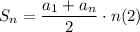
Докажем, что выражение (2) тождественно выражению (1) при
a₁ = -2 и 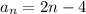 , подставив в (2)
, подставив в (2)
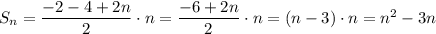
Тождество доказано.
Следовательно, последовательность, определённая суммой 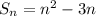 является арифметической прогрессией.
является арифметической прогрессией.
1) Относительная частота попаданий 32/40 = 4/5 = 0,8
2) Вероятность бракованной детали 75/500 = 3/20 = 0,15
3) Он соберет 200*0,85 = 170 кочанов капусты.
4) Опоздали 40 из 300, не опоздали 300-40 = 260 из 300
Вероятность, что ученик не опоздал как минимум 260/300 = 13/15.
Если были ученики, которые опаздывали не один раз, то вероятность, что случайный ученик не опоздал, ещё больше.
Например, если все 40 раз опоздал один ученик, то не опоздали остальные 299.
5) Не более 2 очков - это 1 или 2 очка. Это 33 + 57 = 90 раз.
Частота этого события 90/300 = 3/10 = 0,3.
6) Если даже взять два самых больших числа меньше 10, то есть 9 и 9, все равно сумма будет 18 < 20. Вероятность равна 0.
1. Диета: не больше 5-и тортиков в день:
2. Максимум может съесть 8 тортиков в день;
3. Условие, если 1 день - 8 тортиков,
то 2 следующих дня - по 3 тортика в день;
Если предположить, что с 01.12 до 31.12 сила воли слону не оказала ни разу, то слон съел бы за месяц (в декабре 31 день)
31*5=155 тортиков
Поскольку, по условию, сила воли иногда отказывает, то минимальное количество дней, когда слону отказала сила воли, = 1.
Если предположить, что слон съел максимальное количество тортиков, 8 шт, 31 декабря, то количество съеденного будет
30*5+8=158 тортиков, и диета - закончилась))
Если предположить, что день отказа силы воли пришелся не позже, чем 3 дня до конца декабря, то количество съеденных тортиков будет:
28*5+8+3+3=154 тортика
ответ: 158 тортиков
Воспользуется тем, что сумма первых n членов последовательности равна сумме первых (n-1) членов последовательности и n-ого члена последовательности:
Отсюда выразим n-ый член последовательности:
Найдем его:
Как видно, n-ый член последовательности имеет форму n-ого члена арифметической прогрессии, который обычно записывается так:
Преобразовав, можно получить:
Получаем несложную систему для нашего случая:
Дорешав которую, можно определить какая именно арифметическая прогрессия имелась в виду: