
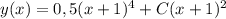
Объяснение:
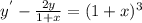
Умножим обе части уравнения
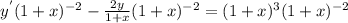
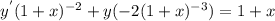


В левой части уравнения производная произведения


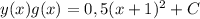

х расстояние между А и В.
х/(2*80) = х/160 ч время потраченное 1 автомобилем на первую половину пути
х/(2*120) = х/240 ч время потраченное 1 автомобилем на вторую половину пути
х/100 ч время потраченное 2 автомобилем на путь
По условию известно, что второй автомобиль, затратил на движение на 6 минут = 6/60 = 1/10 ч меньше первого.
Составим уравнение:
х/160 + х/240 - х/100 = 1/10 (умножим обе части уравнения на 10)
х/16 + х/24 - х/10 = 1 (приведем к общему знаменателю = 240)
(15х + 10х - 24х)/240 = 1
х = 240
ответ. 240 км расстояние между А и В.
10 - 11 классыМатематика 23+12 б Сколькими можно расставить белые фигуры (2 коня, 2 слона, 2 ладьи, ферзь и король) на первой линии шахматной доски (т.е. на полоске 1×8, раскрашенной в черные и белые цвета по порядку: черная клетка, белая клетка, черная клетка и т.д.) так, чтобы слоны стояли на клетках одного цвета, а король стоял рядом с ферзем? Реклама Отметить нарушение AAAntistre 12.11.2016 ответы и объяснения IrkaShevko IrkaShevko Модератор 1) посчитаем, сколько вариантов поставить короля и ферзя: * они занимают две подряд идущие клетки, всего вариантов 7 * мы можем еще поменять в каждом варианте КФ на ФК, получим еще 7 вариантов итого 7+7 = 14 вариантов расстановки короля и ферзя 2) осталось шесть клеток (3 белые, 3 черные), поставим слонов: * выберем любой цвет - 2 варианта * выберем две клетки из трех - 3 варианта итого 2*3 = 6 вариантов поставить слонов 3) поставим двух коней * кони не отличаются, т.к. оба белые * выберем из оставшихся четырех клеток две: C_4^2 = 6 итого 6 вариантов расставить коней 4) поставим ладьи в оставшиеся клетки итого 1 вариант для ладей в итоге для расстановки всех фигур получим ответ
y(x) = (x + x^2/2 + C)(1+x)^2
Объяснение:
Это неоднородное уравнение, решается заменой:
y(x) = u(x)*v(x), тогда y'(x) = u'(x)*v(x) + u(x)*v'(x)
Вынесем за скобки всё, что можно. У нас это только u:
Скобку в левой части приравняем к 0:
Получили уравнение с разделёнными переменными, интегрируем:
ln |v| = 2ln |1+x| = ln (1+x)^2
v(x) = (1+x)^2
Подставляем в уравнение (2):
Делим всё уравнение на (1 + x)^2:
u' = 1 + x
Интегрируем:
u(x) = x + x^2/2 + C
Делаем обратную замену:
y(x) = u(x)*v(x) = (x + x^2/2 + C)(1+x)^2