Пусть вторая труба наполняет бак за х часов, тогда первая наполнит его за х-2 часа. Отсюда производительность первой трубы 1/(х-2), а второй трубы 1/х. Их общая производительность 1/175/60 (2 часа 55 минут - это 175/60 часа) или 60/175. Можно записать уравнение 1/(х-2)+1/х=60/175 1/(х-2)+1/х-60/175=0 (х+(х-2))*175-60х(х-2)=0 350х-350-60х²+120х=0 Для удобства сократим на 10 и умножим на -1 6х²-47х+35=0 D=(-47)-4*6*35=2209-840=1369 x₁=(47-37)/12=10/12=5/6 x₂=(47+37)/12=7 5/6 часа нам не подходит, уж слишком небольшой промежуток времени, в вот 7 часов как раз то, что надо. Значит вторая труба наполняет бак за 7 часов, а первая за 7-2=5 часов.
1. а) значение аргумента равно 3, тогда значение функции:
б) Согласно условию значение функции равно 5, то есть,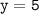
, то значение аргумента найдем, решив следующее уравнение:
в) Подставляя координаты точки В в график уравнения, получим
Раз выполняется тождество, следовательно, график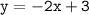
проходит через точку В(-1;5).
2. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки, например: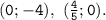
а) значению аргумента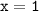
соответствует значение функции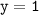 
б) значению функции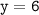
соответствует значение аргумента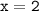 
3. Точки пересечения с осью координат Х. График функции пересекает ось Х при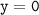
, значит нужно решить уравнение:
Точки пересечения с осью координат У. График пересекает ось У, когда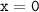
, то есть, подставляя х=0 в график уравнения, получим
4. Раз график функции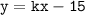
проходит через точку 
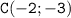, значит значение 
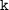найдем, подставив координаты точки C, имеем