Question

36. Решите уравнение: 1) х2 – 5х – 12 = 6; 3) х2 + 8x = -16 – 2x; 2) х2 – 5х – 4 = 10; 4) х2 + х – 2 = 2 – 2x; 6) 9x - x2 = 6 + 2x; 8) x — 2х2 + 7 = -1 – 5x; 5) -х2 + 3х – 12 = — 4x; 7) - x2 + 5х = 18 — 6x; 9) 2x - 3x2 + 8 = -1 - 6x.

Answer 1

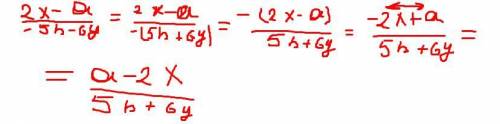
Объяснение:

Решите уравнение:

1) х^2 – 5х – 12 = 6;

х^2 – 5х – 12 -6 =0;

х^2-5х-18 =0;

a=1;  b=-5;  c=-18;

D=b^2-4ac=(-5)^2-4*1*(-18)=25+72=97>0 - 2 корня.

x1,2=(-b±√D)/2a=(-(-5)±√97)/2*1=(5±√97)/2;

x1=(5+√97)/2;

x2=(5-√97)/2.

3) х²+ 8x = -16 – 2x;

x^2+10x+16=0;

по т. Виета

x1+x2=-10;

x1*x2=16;

x1=-2;  x2=-8.

2) х^2-5х-4 = 10;

х^2-5х-14=0;

по т. Виета

x1+x2=5;  x1*x2=-14;

x1=-2;   x2=7.

4) х^2 + х – 2 = 2 – 2x;

x^2+3x-4=0;

по т. Виета

x1+x2=-3;  x1*x2=-4;

x1=1;  x2=-4.

6) 9x - x2 = 6 + 2x;

-x^2+7x-6=0;         [*(-1)]

x^2-7x+6=0;

по т. Виета

x1+x2=7;  x1*x2=6;

x1=1;  x2=6.

8) x — 2х2 + 7 = -1 – 5x;

-2x^2+6x+8=0;                  [:(-2)]

x^2-3x-4=0;

по т. Виета

x1+x2=3;  x1*x2=-4;

x1=-1;  x2=4.

5) -х^2 + 3х – 12 = — 4x;

-x^2+7x-12=0;                     [*(-1)]

x^2-7x+12=0

по т. Виета

x1+x2=7;  x1*x2=12;

x1=3;  x2=4.

7) - x^2 + 5х = 18 — 6x;

-x^2+11x-18=0;                  [*(-1)]

x^2-11x+18=0;

по т. Виета

x1+x2=11;  x1*x2=18;

x1=2;  x2=9.

9) 2x - 3x^2 + 8 = -1 - 6x.​

-3x^2+8x+9=0;            [*(-1)]

3x^2-8x-9=0;

a=3;  b=-8;  c=-9;

D=b^2-4ac=(-8)^2-4*3*(-9)=64+108=172>0 - 2 корня.

x1,2=(-b±√D)/2a=(-(-8)±√172)/2*3=(8±2√43)/6=(4±√43)/3;

x1=(4+√43)/3;

x2=(4-√43)/3.