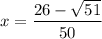3 пары
Объяснение:
Я не буду различать пары вида (a, b) и (b, a).
Запишем в виде НОК(a, b) - НОД(a, b) = 17.
Заметим, что, например, a делится на НОД(a, b) и НОК(a, b) делится на a, значит, НОК(a, b) делится на НОД(a, b), и вся левая часть делится на НОД(a, b). В правой части стоит 17, тогда НОД(a, b) должен быть делителем 17.
17 – простое число, у него только два делителя: 1 и 17. Получаем два случая:
1) НОД(a, b) = 1. Тогда НОК(a, b) = ab = 18. Все возможные разложения 18 на множители: 18 = 1 * 18 = 2 * 9 = 3 * 6. Пара (3, 6) не подходит, для неё НОД равен 3, а две другие – подходят.
2) НОД(a, b) = 17. Тогда НОК(a, b) = 34. Единственная возможность – одно число равно 17, а другое 34.
1) Построим графики функций
и прямую параллельную оси ОХ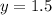 
Графики пересекаются в точке (0.5625; 1.5), где x = 0.5625 - корень данного уравнения
2) Построим график функции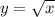
и прямую 
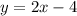проходящую через точки (0;-4), (2;0). Отсюда абсцисса точки пересечения двух графиков 
3) Построим график функции y = √x и прямую y = 2 - 4x, проходящую через точки (0;2), (1;-2). Абсцисса точки пересечения двух графиков равна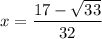
4) Построим график функции y = 0.4√x и прямую y = 1 - 2x, проходящую через точки (0;1), (1;-1). Абсцисса точки пересечения двух графиков равна