Формула решения квадратного уравнения!
ax^2+bx+c=0
x1=(-b+кор.кв.( b^2-4ac))/2a
x2=(-b-кор.кв.( b^2-4ac))/2a
где:
^2- значит в квадрате!
кор.кв.( b^2-4ac) - корень квадратный из выражения (b в квадрате -4*a*c)
1)5x^2-7x+2=0
x1=(7+кор.кв(49-40))/10=(7+3)/10= 1
х2=(7-кор.кв(49-40))/10=(7-3)/10= 0,4
2)3x^2+5x-2=0
x1=(-5+кор.кв.(25-24))/6=(-5+1)/6=-4/6= -2/3
x2=(-5-кор.кв.(25-24))/6=(-5-1)/6=-6/6= -1
3)2x^2-7x+3=0
x1=(7+кор.кв.(49-24))/4=(7+5)/4=12/4= 3
x2=(7-кор.кв.(49-24))/4=(7-5)/4=2/4= 1/2
4)3x^2+2x-5=0
x1=(-2+кор.кв(4+60))/6=(-2+8)/6= 1
x2=(-2-кор.кв(4+60))/6=(-2-8)/6=-10/6= -1(2/3)
5)5x^2-3x-2=0
x1=(3+кор.кв.(9+40))/10=(3+7)/10=10/10= 1
x2=(3-кор.кв.(9+40))/10=(3-7)/10=-4/10= -0,4
Вероятность того, что выбранный из 10 юношей окажется одним из двух, имеющим первый дан:
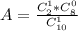
Вероятность того, что выбранная из 4 девушек окажется той единственной. имеющей первый дан:
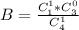
Общую вероятность можно посчитать перемножив вероятность для юношей и для девушек - A*B
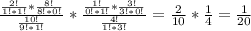
Это если "по-умному". В лоб:
Вероятность выбрать из 10 юношей юношу с первым даном = 2/10, т.к. юношей с первым даном 2, а всего - 10. Для девушек - 1/4. т.к. с первым даном 1, всего - 4. Общая вероятность получается перемножением. ответ такой же: 1/20
Так как произведение крайних членов равно произведению средних членов мы можем решить что так:
1. (2,4*0,5):0,8 =1,5
2. (12*75):15=60